Action Representation

How is a robot’s action space represented when you try to train a model? Some ideas presented in Diffusion Policy paper.

• More generally, what are the outputs of a robot’s policy? Does that matter? Yes

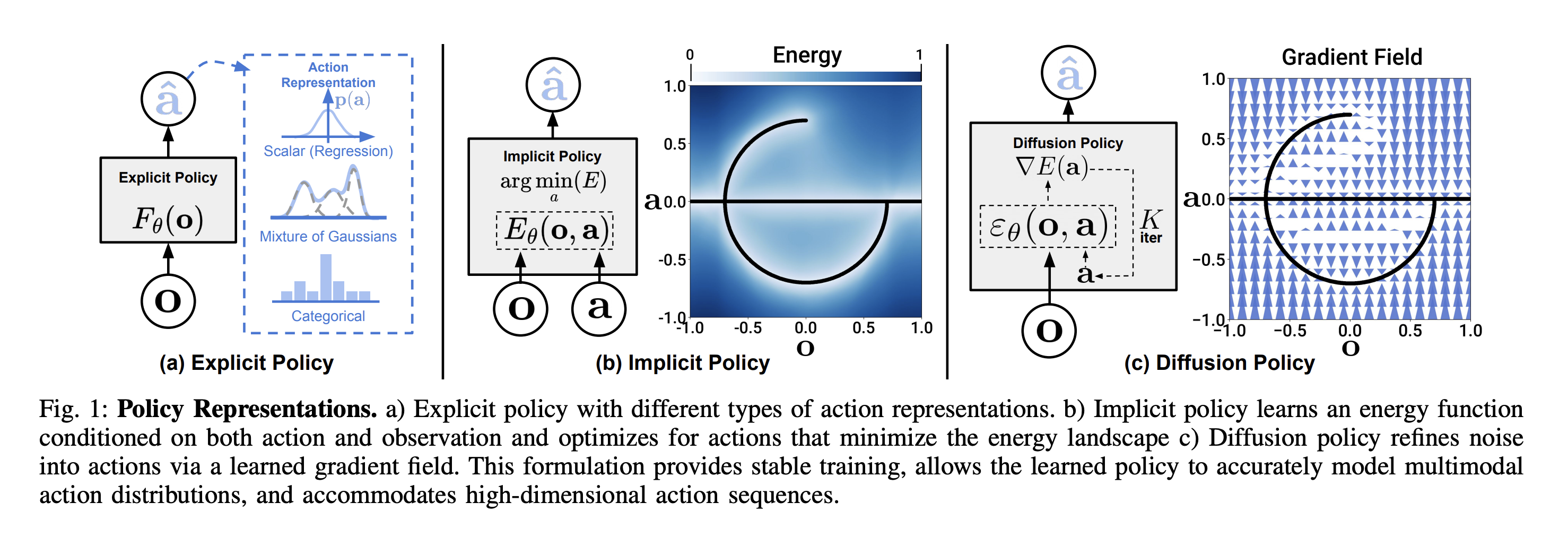
2 general categorizations:

1. Explicit Policy
   • Scalar output
   • Mixtures of Gaussians
   • Quantized (categorical) actions
2. Implicit Policy
   1. Energy-based models
   2. Diffusion-based models

So what does a model actually use?

ACT and Pi0 use an explicit policy, they directly predict the action given a state.

• Explicit Policy: Directly maps states to actions. You can sample sample actions and compute the probability π(a∣s)
• Implicit policy: Defines actions indirectly—you can sample from the policy but can’t compute the exact probability.

Explicit Policy

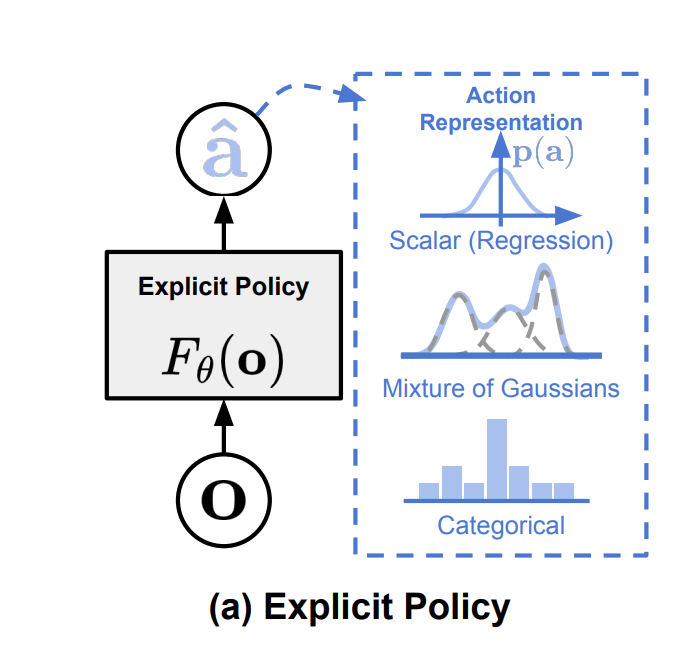
1. Scalar

• Simplest form: Output is a deterministic or probabilistic scalar for each action dimension.
• Often used in classical control or basic reinforcement learning setups.

[0.1, 0.2, ..., -0.1]  # Direct joint commands

2. Mixture of Gaussians

• Rather than a single scalar, we model the action as a mixture of distributions.
• Good for capturing multi-modal behaviors (e.g., multiple valid trajectories).

Output:
A set of $M$ Gaussians over the 7D action space.
${\left\{({\mu }_i,{\Sigma }_i,w_i)\right\}}_{i=1}^M,{\mu }_i\in {\mathbb{R}}^7,{\Sigma }_i\in {\mathbb{R}}^{7\times 7},w_i\in [0,1]$

[
    {"mean": [0.1, 0.2, ..., 0.0], "cov": [[...]], "weight": 0.6},
    {"mean": [-0.2, 0.1, ..., 0.4], "cov": [[...]], "weight": 0.4}
]

3. Quantized (Categorical) Actions

• Discretize the action space into $K$ bins per dimension (like bucketing).
• Output is a categorical distribution over these bins.
• Effective when action precision is low or discrete behaviors are sufficient.

Output:
$p(a)\in {\mathbb{R}}^K\text{(e.g., 100 bins)}$

[0.01, 0.02, ..., 0.3, ..., 0.01]  # Probabilities over discrete bins

• This is essentially what I did when I worked on my Poker AI to generate different clusters of distributions

Implicit Policy

Unlike explicit policies which output actions directly, implicit policies output samples drawn from a complex, often intractable distribution (e.g., energy-based or diffusion-based).

1. Energy-Based Models

• Define an energy function $E(x)$ where low-energy configurations are preferred.
• Actions are sampled by finding low-energy regions (e.g., via Langevin dynamics).
• Often hard to train, but good for flexible, high-capacity distributions.

2. Diffusion-Based Models (e.g., Diffusion Policy)

• Start from random noise in ${\mathbb{R}}^7$, and denoise iteratively over $K$ steps.
• Each step refines the sample toward a realistic, valid action.

Output:
Final denoised action vector in ${\mathbb{R}}^7$.

# Step-by-step denoising
Start: [0.5, -0.3, ..., 0.1]
After diffusion → [0.12, 0.08, ..., -0.05]

• Diffusion captures multi-modal and complex correlations in the action space without explicitly modeling a likelihood.