DFS/BFS Tree

Introduced in CS341. Quite useful in Competitive Programming.

For example, this problem: https://codeforces.com/problemset/problem/1666/L

• You build a bunch of DFS trees, sexy solution by jiangly https://codeforces.com/contest/1666/submission/153533633

• Source: https://notes.eddyerburgh.me/data-structures-and-algorithms/algorithms/graph-traversal

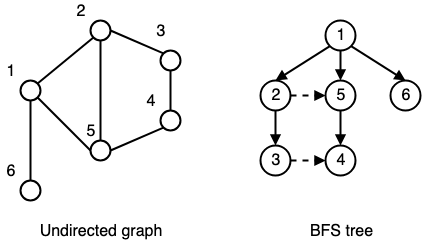
BFS tree (page 16/21)

Definition: the BFS tree $T$ is the subgraph made of:

• all vertices $w$ such that $parent[w]\ne NIL$
• all edges $\{w,parent[w]\}$, for $w$ as above (except $w=s$)

How do we create a BFS tree?

• Using the algorithm above, which ensures that the properties described hold
• parent[w] keeps track of the parents

Lemma (page 16/21)

The BFS tree $T$ is a tree.

• Note that the BFS tree is not always unique

Subclaims

• The levels in the queue are non-decreasing
• For all vertices $u,v$, if there is an edge $\{u,v\}$, then $level[v]\le level[u]+1$

Shortest path from BFS Tree (18/21)

For all $v\in G$:

• there is a path $s\to v$ in $G$ iff there is a path $s\to v$ in $T$
• if so, the path in $T$ is a shortest path and $level[v]=dist(s,v)$