Beta Distribution

Let $X\sim Beta(\alpha ,\beta )$., then the PDF of Beta Distribution is given by $f(x)=\frac{\Gamma (\alpha +\beta )}{\Gamma (\alpha )\Gamma (\beta )}{x}^{\alpha -1}(1-x{)}^{\beta -1},\text{for }0\le x\le 1$

$\alpha$ and $\beta$ will determine the shape of the distribution. Conceptually,

• $\alpha$ represents number of successes
• $\beta$ represents number of failures

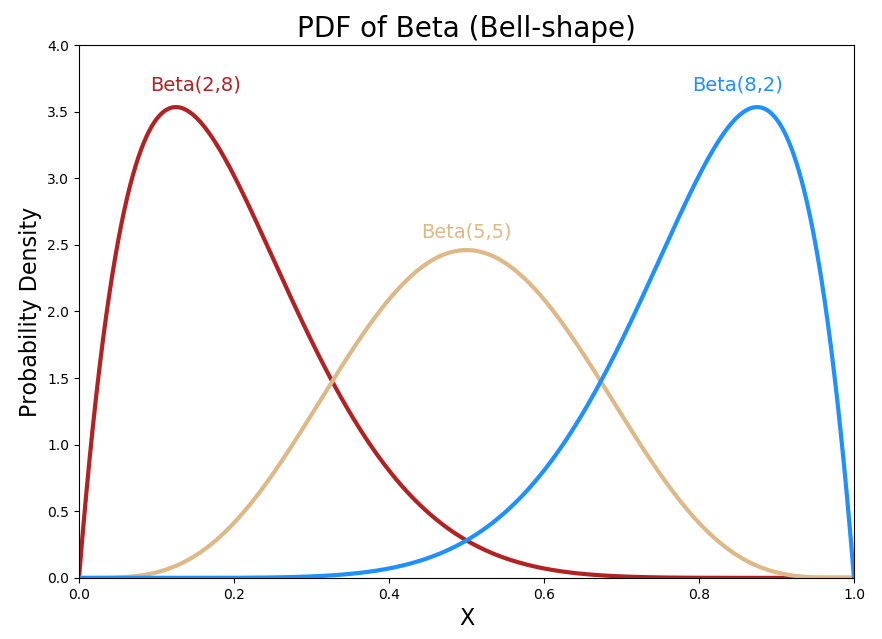
Cool Visualization

Expectation and variance:

• $E(X)=\frac{a}{a+b}$
• $Var(X)=\frac{ab}{(a+b{)}^2(a+b+1)}$

As you increase $\alpha$ and $\beta$, the graph becomes spikier, which results more confidence in the mean.

Related

• Binomial Distribution