Birthday Paradox

This is a very interesting idea that I saw from the internet, and was again reintroduced to after reading the Competitive Programmer’s Handbook.

The birthday paradox states that if there are $n$ people in a room, the probability that some two people have the same birthday is large even if $n$ is quite small.

→ The explanation for this is that the days at which people are born is not uniformly distributed. A lot of people are born during certain days of the year.

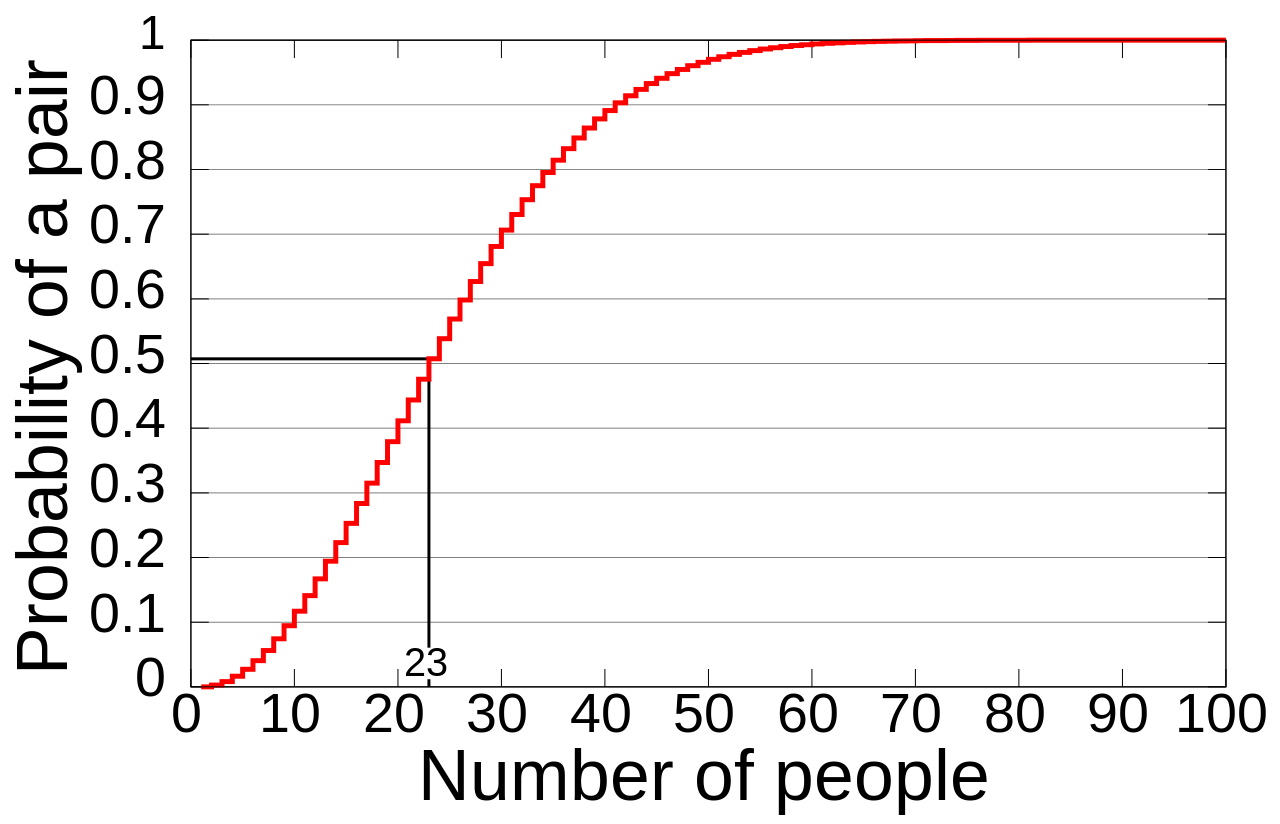In probability theory, the birthday problem asks for the probability that, in a set of $n$ randomly chosen people, at least two will share a birthday. The birthday paradox is that, counterintuitively, the probability of a shared birthday exceeds 50% in a group of only 23 people.