Curve Sketching

I understand these concepts (increasing, decreasing, maximum, minimum, etc.) at a very high level, but it is useful to define them precisely.

High level of $f^{\prime }(x)$ and $f^{\prime \prime }(x)$

Intuitively, $f^{\prime }(x)$ represents the rate of change of the values of $f(x)$ (or think of it as the slope of the tangent lines to $f(x)$. We use $f^{\prime }(x)$ to understand when a function is increasing and decreasing, as well as find extrema values.

$f^{\prime \prime }(x)$ is a bit harder to grasp. It describes the rate of change of the tangent line to $f(x)$. Think of it related to Newton’s law, $s^{\prime \prime }(t)=v^{\prime }(t)=a(t)$ The second derivative provides information about the curve behavior, which we call concavity.

Increasing and Decreasing, Monotonic

A function $f$ is increasing if $f(x_2)>f(x_1)$ whenever $x_2>x_1$. A function $f$ is decreasing if $f(x_2)<f(x_1)$ whenever $x_2>x_1$. We can define these in terms of the derivative,

title: Increasing
If $f'(x)>0$ for all $x \in I$, we say that $f(x)$ is *increasing* on $I$.

title: Decreasing
If $f'(x)<0$ for all $x \in I$, we say that $f(x)$ is *decreasing* on $I$ .

Note: The converse is NOT true. If $f$ is increasing we may still find that $f^{\prime }(x)=0$ at some isolated points.#idontunderstand

title: Monotonic
If $f$ is either increasing or decreasing on $I$, we may sat that $f$ is *monotonic* on $I$. 

Maxima and Minima (Extrema), Critical Point

A function $f$ has an absolute maximum at $c$ if $f(c)\ge f(x)$ for all $x$ in the domain of $f$. A function $f$ has an absolute minimum at $c$ if $f(c)\le f(x)$ for all $x$ in the domain of $f$.

title: Critical Point
 A *critical point* of $f$ is a point at which $f'(c)=0$  or $f'(c)$ does not exist.

It's important to note that some functions have no extrema, such as $f(x) = x$ defined on $\mathbb{R}$, or $f(x)=x$ on the open interval $(-1,3)$. It would work if $f(x) = x$ is defined on the closed interval $[-1,3]$.

Algorithm for identifying Global Extrema: Closed Interval Method

We use the idea that if $c$ is a global maximum or minimum of $f$, one of three things must be true:

1. $f^{\prime }(c)=0$ (a critical point)
2. $f^{\prime }(c)$ is undefined (a critical point)
3. $c$ is an endpoint of the interval.

Thus, we develop an algorithm for this.

title:The Closed Interval Method
Let $f(x)$ be a continuous function defined over a closed interval $I=[a,b]$. The global extrema (maximum and minimum values) can be determined using the following steps.
 
1.  Determine the derivative $f'(x)$.
2.  Determine all critical points $(c_1,\dots,c_n)$ that lie within the interval $I$.
3.  Evaluate $f(x)$ at the critical points and the endpoints (i.e., at each of $a$,$b$, and $(c_1,\dots,c_n)$).
4.  Compare: The largest output value obtained from the previous step is the global maximum; the smallest output value is the global minimum.

Algorithm for identifying Local Extrema: First Derivative Test

title: First Derivative Test
If a function $f(x)$ has a *critical point* at $x=c$, then we have the following:
-   If the sign of $f'(x)$ does not change upon crossing $c$, then $c$ is neither a local maximum nor a local minimum.
-   If $f'(x)>0$ for $x<c$ and $f'(x)<0$ for $x>c$, then $c$ is a *local maximum*.
-   If $f'(x)<0$ for $x<c$ and $f'(x)>0$ for $x>c$, then $c$ corresponds to a *local minimum*.

The second derivative test also works.

title: Second Derivative Test
If $f'(c)=0$ and $f''(c)<0$, then $f(x)$ has a *local maximum* at $x=c$.
If $f'(c)=0$ and $f''(c)>0$, then $f(x)$ has a *local minimum* at $x=c$.

Concavity, Inflection Point

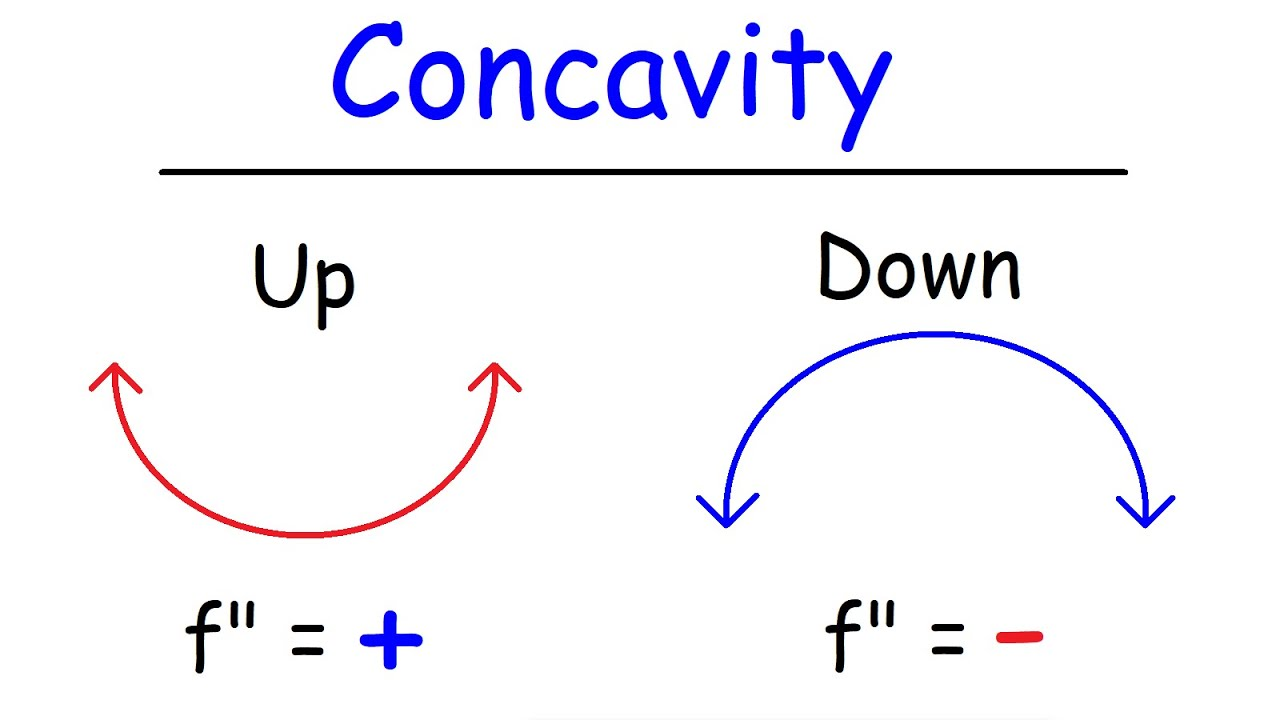
title: Concavity
If $f''(x) > 0$ on some interval $I$, we say that $f(x)$ is *concave up* on $I$.
If $f''(x) < 0$ on some interval $I$, we say that $f(x)$ is *concave down* on $I$.

If the concavity of $f(x)$ changes at a point $(x_0,f(x_0))$, then we call this point an inflection point.

title: Point of Inflection
For a function $f(x)$ defined on domain $D$, $c \in D$ is a *point of inflection* of $f(x)$ if the following are true:
 
1. $f''(c)=0$ or $f''(c)$ is undefined and
2.  $f''(x)$ switches signs (from positive to negative or vice versa) when crossing $c$.

Related

• Function