Differential Equation (DE)
Definition 1: Independent and Dependent Variables and Parameters
- The dependent variable(s) of a DE are the unknown functions that we want to solve for i.e. , , etc.
- The independent variable(s) of a DE are the variable(s) that the independent variable(s) depend on i.e. , , etc.
- A parameter is a term that is an unknown but is not an independent or dependent variable i.e. etc.
Definition 2: Order of a DE
The order of a DE is the order of the highest derivative.
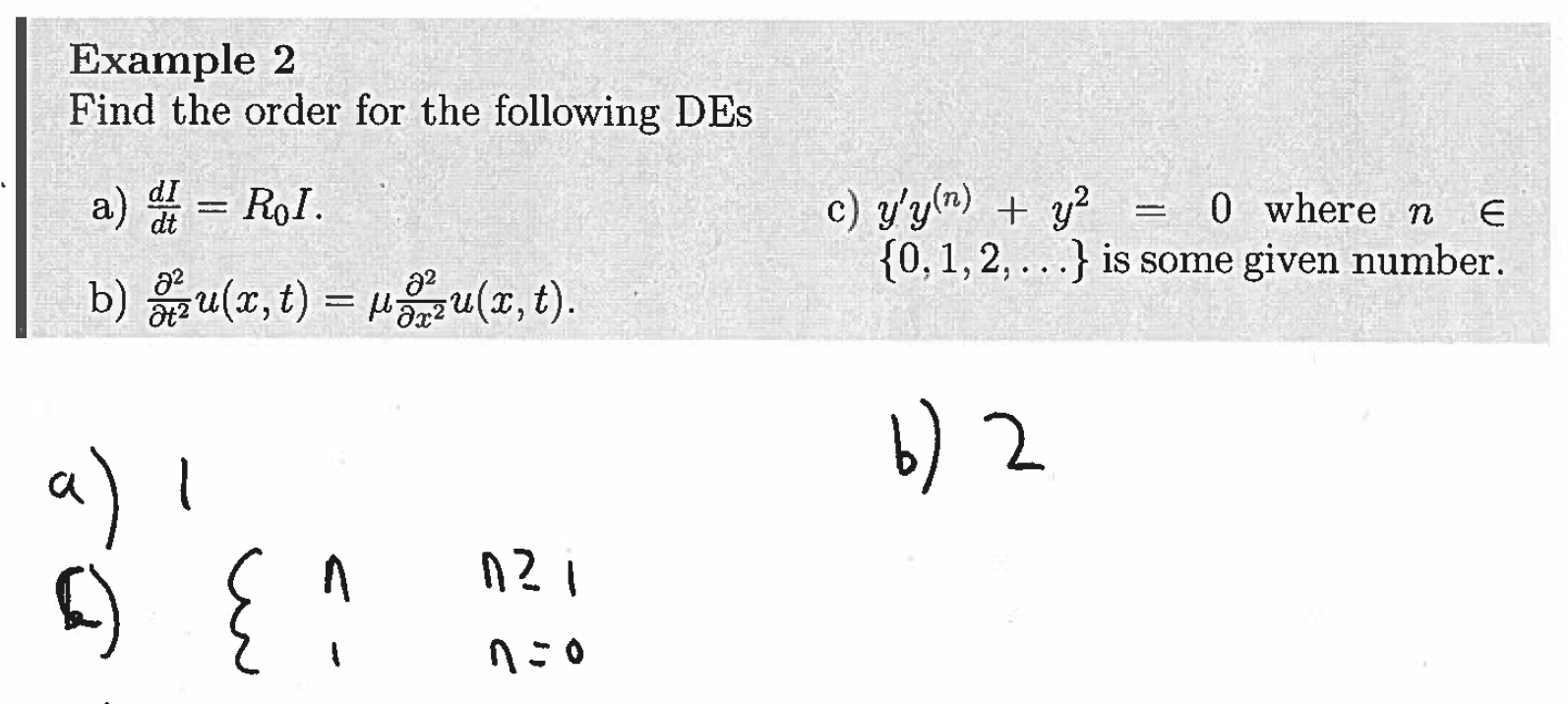
Definition 3: ODEs and PDEs
A DE is an Ordinary Differential Equation (ODE) if it only contains ordinary derivatives (i.e. no partial derivatives).
A DE is a Partial Differential Equation (PDE) if it contains at least one partial derivative of a independent variable.

Definition 4: Linear and nonlinear DEs
A DE that contains no products of terms involving the dependent variable(s) is called linear.
If a DE is not linear then it is nonlinear.
