Flows and Cuts

Ford-Fulkerson Algorithm

The Ford–Fulkerson algorithm is a very straightforward method to find the Maximum Flow in a graph.

Extra Terminology:

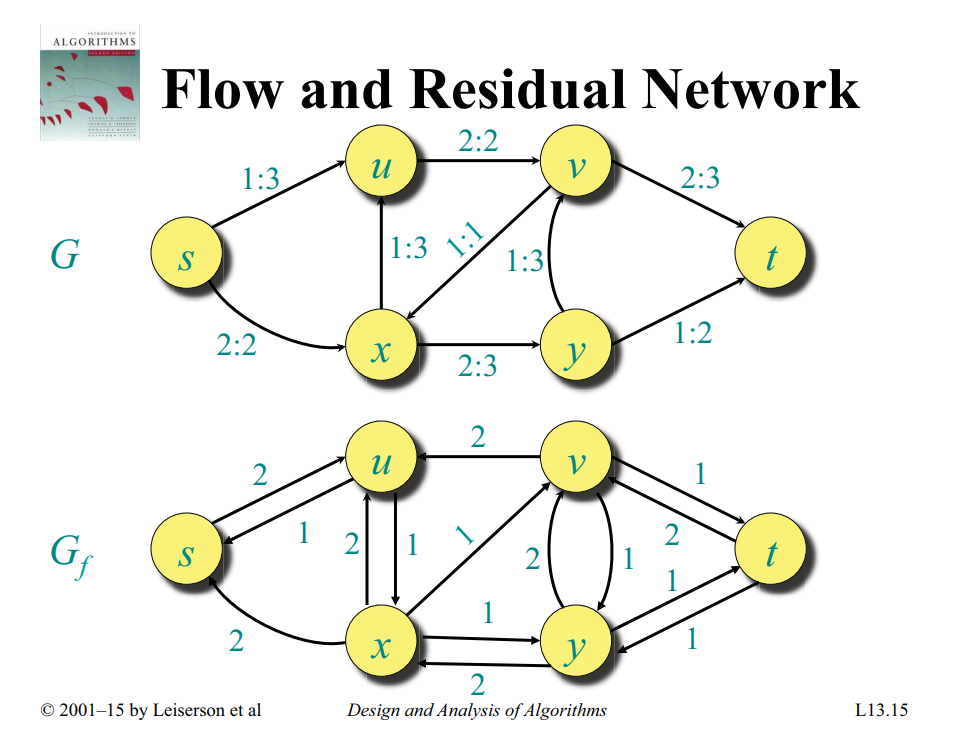
• A residual capacity of an directed edge is the capacity minus the flow, i.e. $c_f(u,v)=c(u,v)-f(u,v)>0$
• The residual graph/network $G_f=(V,E_f)$ is the graph with strictly positive residual capacities
• An augmenting path is any path from $s$ to $t$ in the residual graph $G_f$

The Ford-Fulkerson method works as follows.:

1. For all $u,v\in V$, set $f(u,v)=0$
2. While an augmenting path $p$ in $G_f$ exists, for all $u,v\in p$, augment $f(u,v)$ by $C={\min }_{(u,v)\in p}(c_f(u,v))$
   • we increase $f((u,v))$ by $+C$ and decrease $f((v,u))$ by $-C$ for every edge $(u,v)\in p$
3. Repeat until an augmenting path doesn’t exist anymore

When the algorithm cannot increase the flow anymore, the maximum flow has been found.

Important

You can shrink the flow. You can represent the shrinkage of the flow by a reverse edge in the residual network.

If there is a flow $f(u,v)=x>0$, then you make $c_f(v,u)=x$ (but you need to remember that this is a reverse flow, because in the actual flow network you can’t make this flow go in the $(v,u)$ direction). See code for implementation.

See this example:

Edmonds-Karp algorithm

Edmonds-Karp algorithm is an implementation of the Ford-Fulkerson method that uses BFS for finding augmenting paths in $O(V{E}^2)$ time.

The intuition is, that every time we find an augmenting path one of the edges becomes saturated, and the distance from the edge to s will be longer if it appears later again in an augmenting path. The length of the simple paths is bounded by V.

Implementation

The matrix capacity stores the capacity for every pair of vertices. adj is the adjacency list of the undirected graph, since we have also to use the reversed of directed edges when we are looking for augmenting paths.

The function maxflow will return the value of the maximal flow. During the algorithm, the matrix capacity will actually store the residual capacity of the network. The value of the flow in each edge will actually not be stored, but it is easy to extend the implementation - by using an additional matrix - to also store the flow and return it.

int n;
vector<vector<int>> capacity;
vector<vector<int>> adj;
 
int bfs(int s, int t, vector<int>& parent) {
    fill(parent.begin(), parent.end(), -1);
    parent[s] = -2;
    queue<pair<int, int>> q;
    q.push({s, INF});
 
    while (!q.empty()) {
        int cur = q.front().first;
        int flow = q.front().second;
        q.pop();
 
        for (int next : adj[cur]) {
            if (parent[next] == -1 && capacity[cur][next]) {
                parent[next] = cur;
                int new_flow = min(flow, capacity[cur][next]);
                if (next == t)
                    return new_flow;
                q.push({next, new_flow});
            }
        }
    }
    return 0;
}
 
int maxflow(int s, int t) {
    int flow = 0;
    vector<int> parent(n);
    int new_flow;
 
    while (new_flow = bfs(s, t, parent)) {
        flow += new_flow;
        int cur = t;
        while (cur != s) {
            int prev = parent[cur];
            capacity[prev][cur] -= new_flow;
            capacity[cur][prev] += new_flow;
            cur = prev;
        }
    }
 
    return flow;
}

Extra Constraints

Maximum flow with vertex capacities