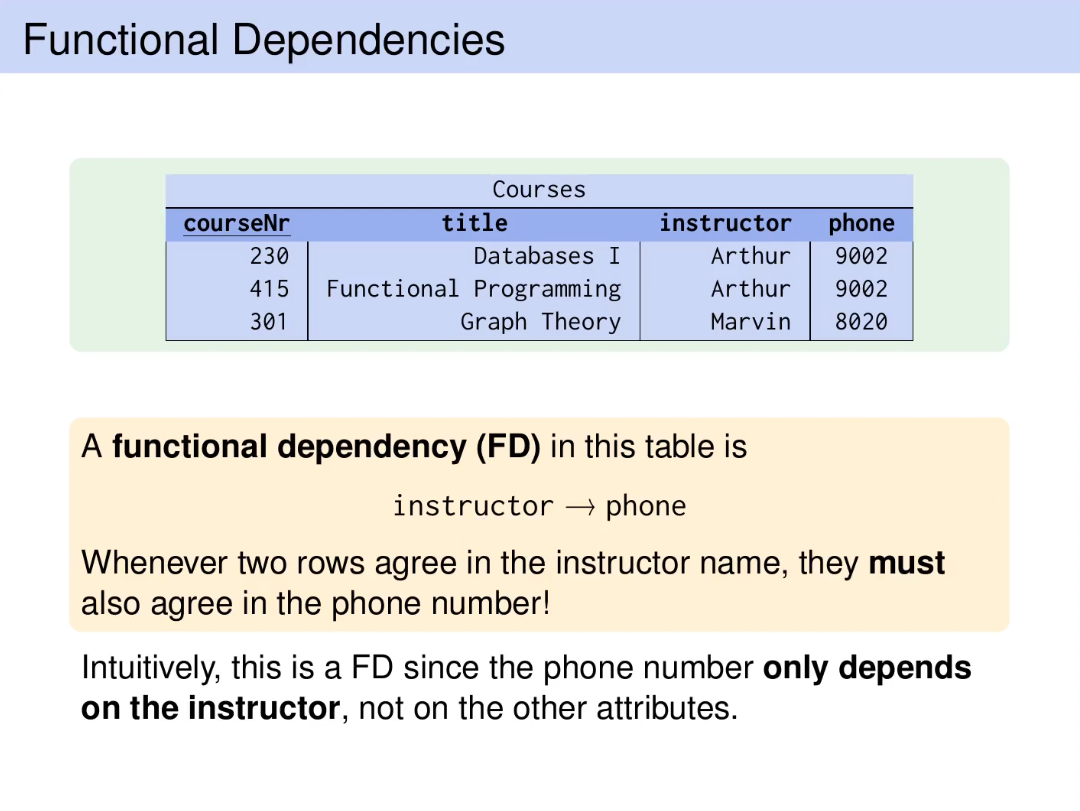
Functional Dependency (FD)

A small fragment of the variety of equality generating dependencies in RC over a single table have proven to be ubiquitous in conceptual design.

Resources

• Watch Database Tutorial 6 onwards

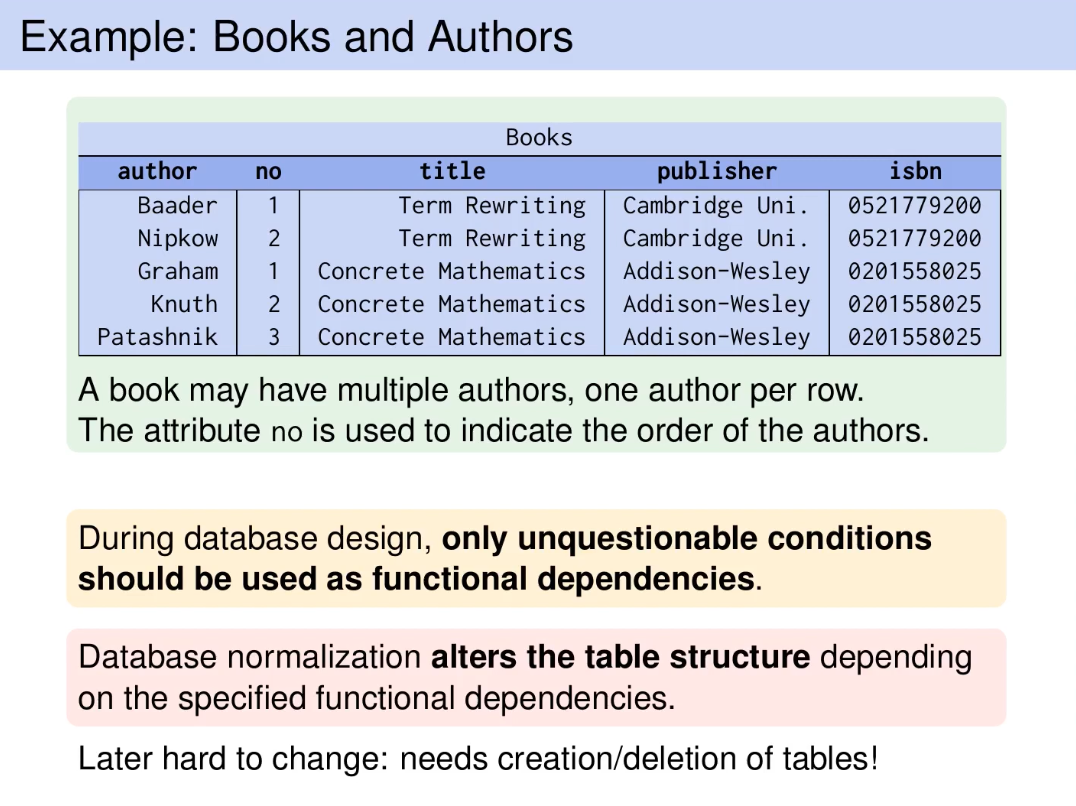
FDs are a generalization of keys and a central part of relational database design theory. FD defines what relation is in normal form.

Two different normal forms:

• Third Normal Form
• Boyce-Codd Normal Form (BCNF)

Danger

Usually, a sign of bad database design if a schema contains relations that violate the normal form.

If a normal form is violated, it means that

• data is stored redundantly
• information about different concepts intermixed

What is the connection between FDs and keys?

Keys ARE functional dependencies.

CS348

I personally think these notes are garbage. Use the notes above.

“X uniquely determines Y” / “X functionally determines Y”

NOT an Implication

I repeat, this is not an implication, even though the notation seems the same. The context is different.

Armstrong’s Axioms

ChatGPT

In the context of databases, an FD or Functional Dependency is a constraint between two sets of attributes in a relation from a database.

Given a relation R, a set of attributes X in R is said to functionally determine another set of attributes Y, also in R, (written $X\to Y$) if and only if each X value is associated with precisely one Y value.

For example, in a Student table, StudentID → FirstName would mean that each StudentID is associated with exactly one FirstName.

A trivial Functional Dependency (FD) is a dependency in which a set of attributes functionally determines a subset of itself. If you have a set of attributes X, and Y is a subset of X, then Y is trivially functionally determined by X. The formal notation for this would be $X\to Y$, where $Y\subseteq X$.

• Ex: Consider a relation with attributes {A, B, C}. Here, {A, B} → A is a trivial functional dependency, because A is a subset of {A, B}.