Graph Edge

Learned in CS341.

White Path Lemma (5/19)

When we start exploring a vertex $v$, any $w$ that can be connected to $v$ by an unvisited path will be visited during $explore(v)$.

• This seems very similar to one of the lemmas from DFS with the iff, but this is cuz $explore$ is a new function introduced for DFS, which calls iself recursively

6/19

If $w$ is visited during $explore(v)$, there is a path $v\to w$.

• use the same proof as BFS by induction. Shouldn’t this be a IFF?

9/19

All edges in $G$ connect a vertex to one of its descendants or ancestors.

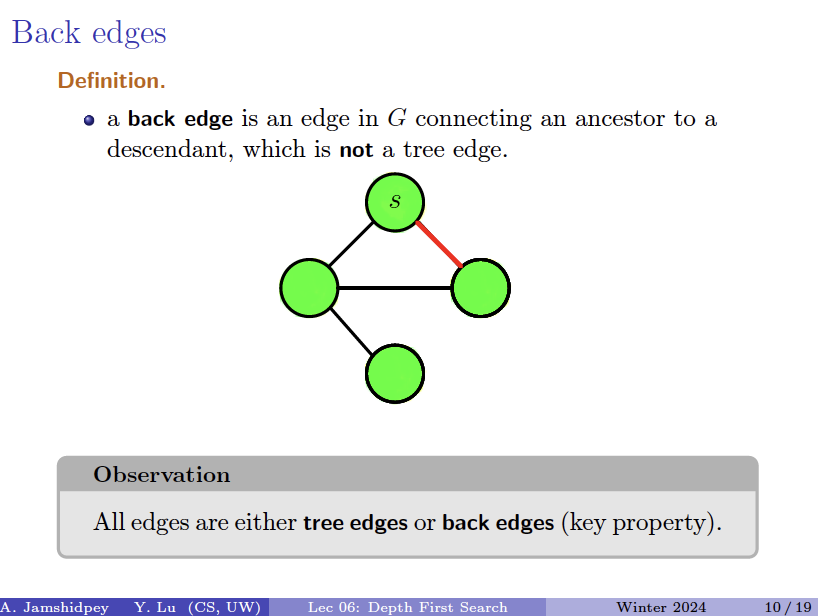
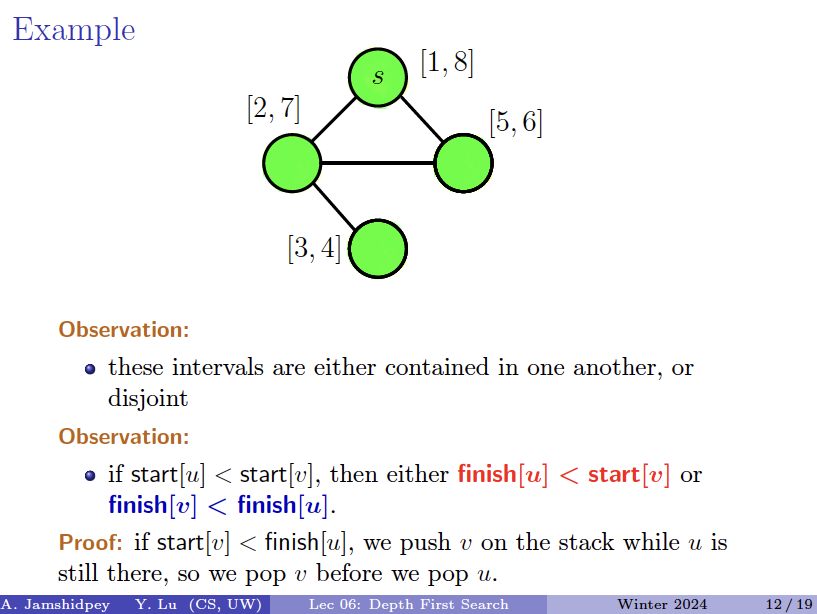
It’s helpful to keep track of the start and finish times.

Then we talk about the cut vertex

Suppose we have a DFS forest. Edges of G are one of the following:

• tree edges
• back edges: from descendant to ancestor
• forward edges: from ancestor to descendant (but not tree edge)
• cross edges: all others

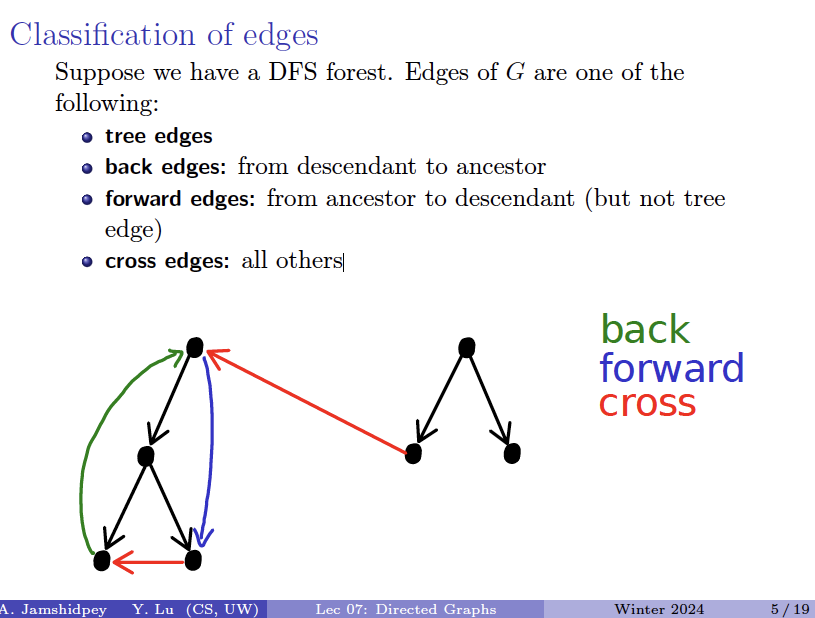
• These new categories of edges exist because we are now working in a directed graph. For an undirected graph, it would only be tree edges and back edges

7/19

$G$ has a cycle if and only if there is a back edge in the DFS forest.

10/19

Suppose that $V$ is ordered using the reverse of the finishing order: $v<w⟺finish[w]<finish[v]$.

This is a topological order.