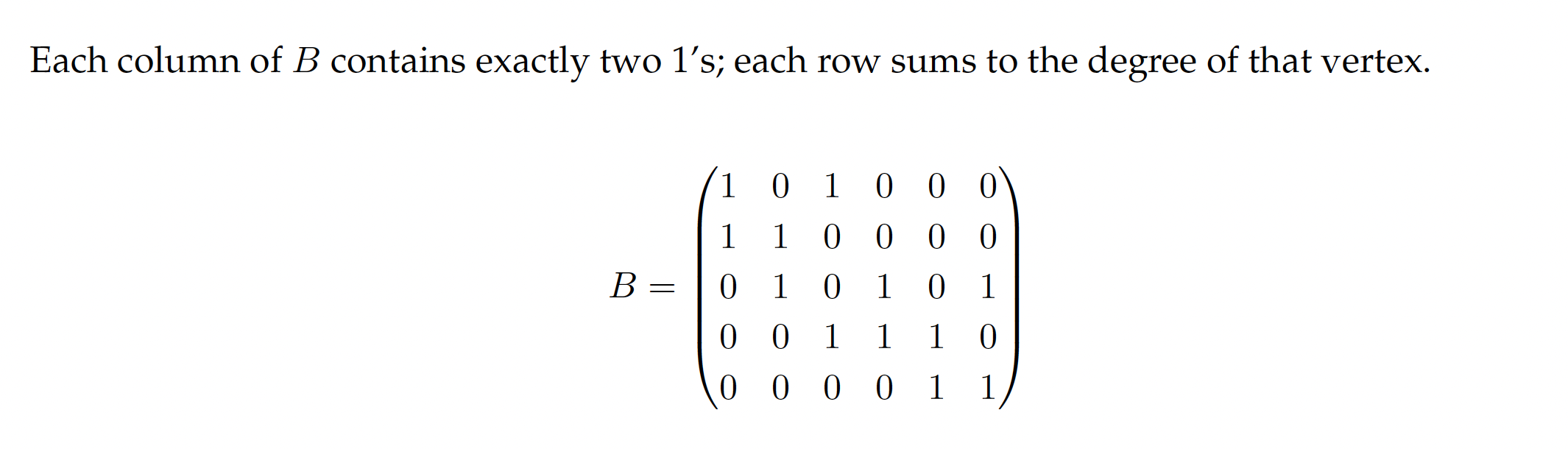Graph

Graph Representation

3 popular ways to implement:

1. Adjacency list representation (most popular)
2. Adjacency matrix representation
3. Edge list representation

Adjacency List Representation

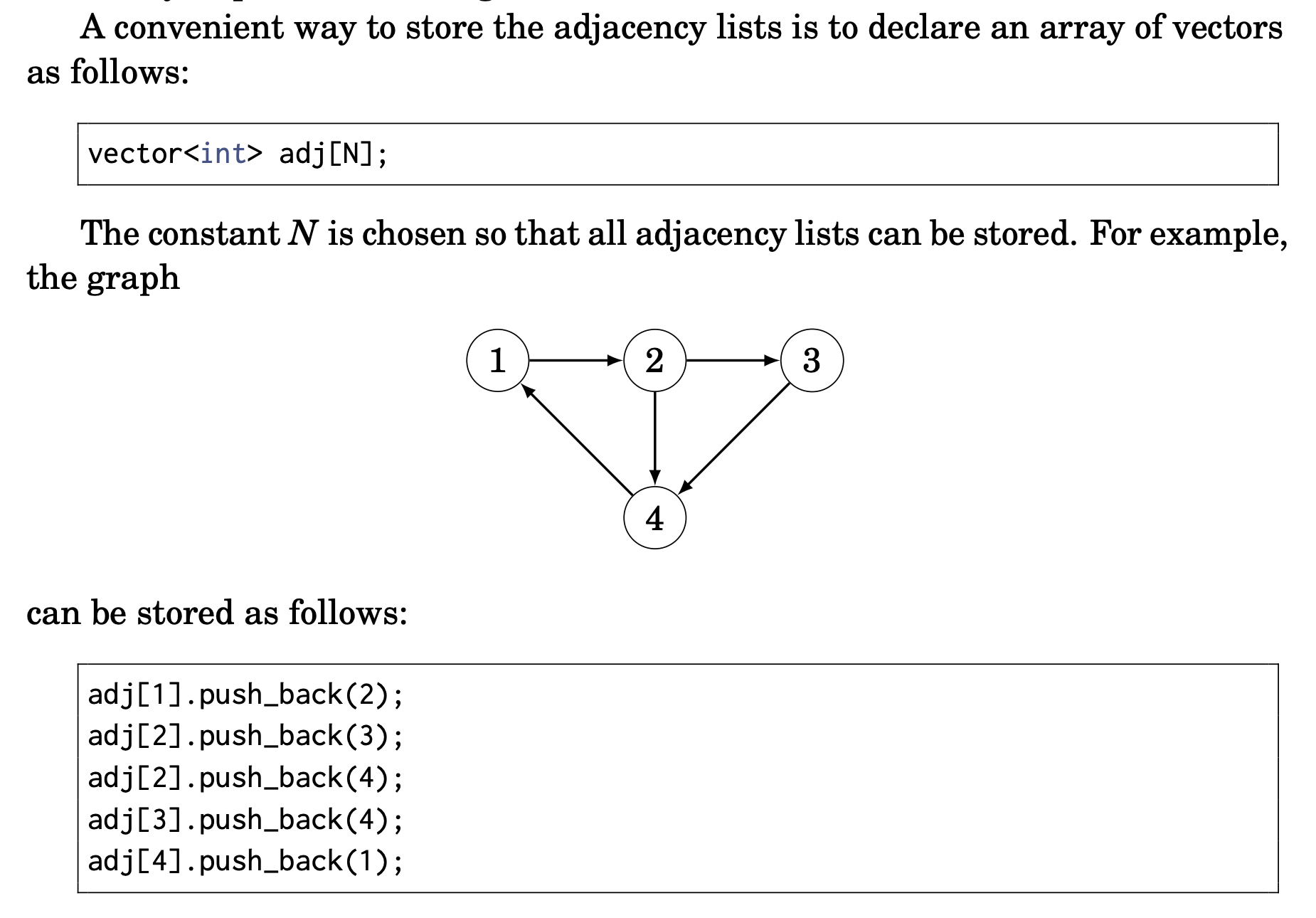
Use an array of vectors.

vector<int> adj[N];

The indices of the array represent the node number, while the actual value of the array are vectors of the other nodes that the current node is connected to.

For a weighted graph, the structure can be extended by using vectors of pairs:

vector<pair<int, int>> adj[N];

With adjacency lists is that we can efficiently find the nodes to which we can move from a given node through an edge. Ex:

for (auto u : adj[s]) { 
	// process node u 
}

Adjacency Matrix Representation

An adjacency matrix is a two-dimensional array that indicates which edges the graph contains.

int adj[N][N];

Each value adj[a][b] indicates whether the graph contains an edge from node a to node b

• adj[a][b] = 1 if there is an edge
• adj[a][b] = 0 if no edges

If weighted, use the value of the weight instead of 1 when storing the edge value.

Edge List Representation

vector<pair<int,int>> edges;
edges.push_back({1,2}); 
edges.push_back({2,3}); 
edges.push_back({2,4}); 

For Weighted edges, add a 3rd value for each edge representing edge weight.

vector<tuple<int, int, int>> edges;
edges.push_back({1,2,5}); 
edges.push_back({2,3,1}); 
edges.push_back({2,4,1}); 

MATH239

Below is some more formal notation as I saw in MATH239.

Adjacency Matrix

The adjacency matrix of a graph with vertices $\{v_1,...,v_n\}$ is the $n\times n$ matrix $A$ where

$A_{ij}=\{\begin{array}{ll}1,& \text{if }{v}_i\text{ and }{v}_j\text{ are adjacent},\\ 0,& \text{otherwise.}\end{array}$

Incidence Matrix

The incidence matrix of a graph with vertices $\{v_1,...,v_n\}$ and edges $e_1,...,e_m$ is the $n\times m$ matrix $B$ where

$B_{ij}=\{\begin{array}{ll}1,& \text{if vertex }{v}_i\text{ is incident with edge }{e}_j,\\ 0,& \text{otherwise.}\end{array}$