Inclusion-Exclusion Principle

This is super helpful to solve lots of problems. You can use the same idea in Probability. For two sets, we have $|A\cup B|=|A|+|B|-|A\cap B|$ For three sets, we have $|A\cup B\cup C|=|A|+|B|+|C|-|A\cap B|-|A\cap C|-|B\cap C|+|A\cap B\cap C|$

For four sets, you follow the same pattern with $|D|$, and add $-|A\cap B\cap C\cap D|$ at the end.

For Probability from STAT206

title: Theorem
Given two events, $A$ and $B$,
$$P(A \cup B)= P(A) + P(B) - P(A \cap B)$$
 
Given three events, $A$, $B$ and $C$, 
$$P(A \cup B \cup C)= P(A) + P(B) + P(C) - P(A \cap B) - P(A \cap C) - P(B \cap C) + P(A \cap B \cap C)$$

Intuition

The intuition is that we subtract to avoid double counting. 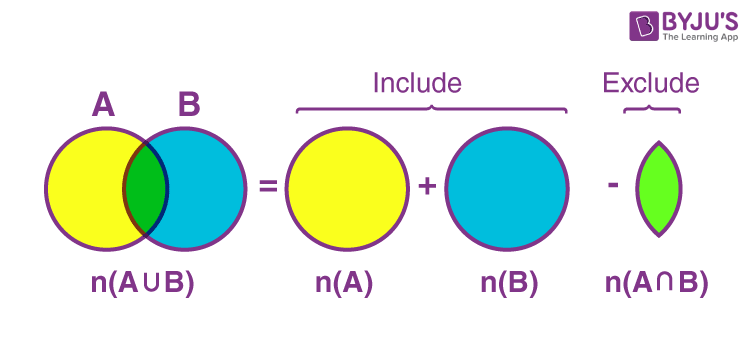When we add these two sets together, we are double counting $A\cap B$, so we subtract it so count exactly once.

For three sets, subtracting the intersections would also remove all of the $A\cap B\cap C$, so we need to add it in again. See the diagram below:

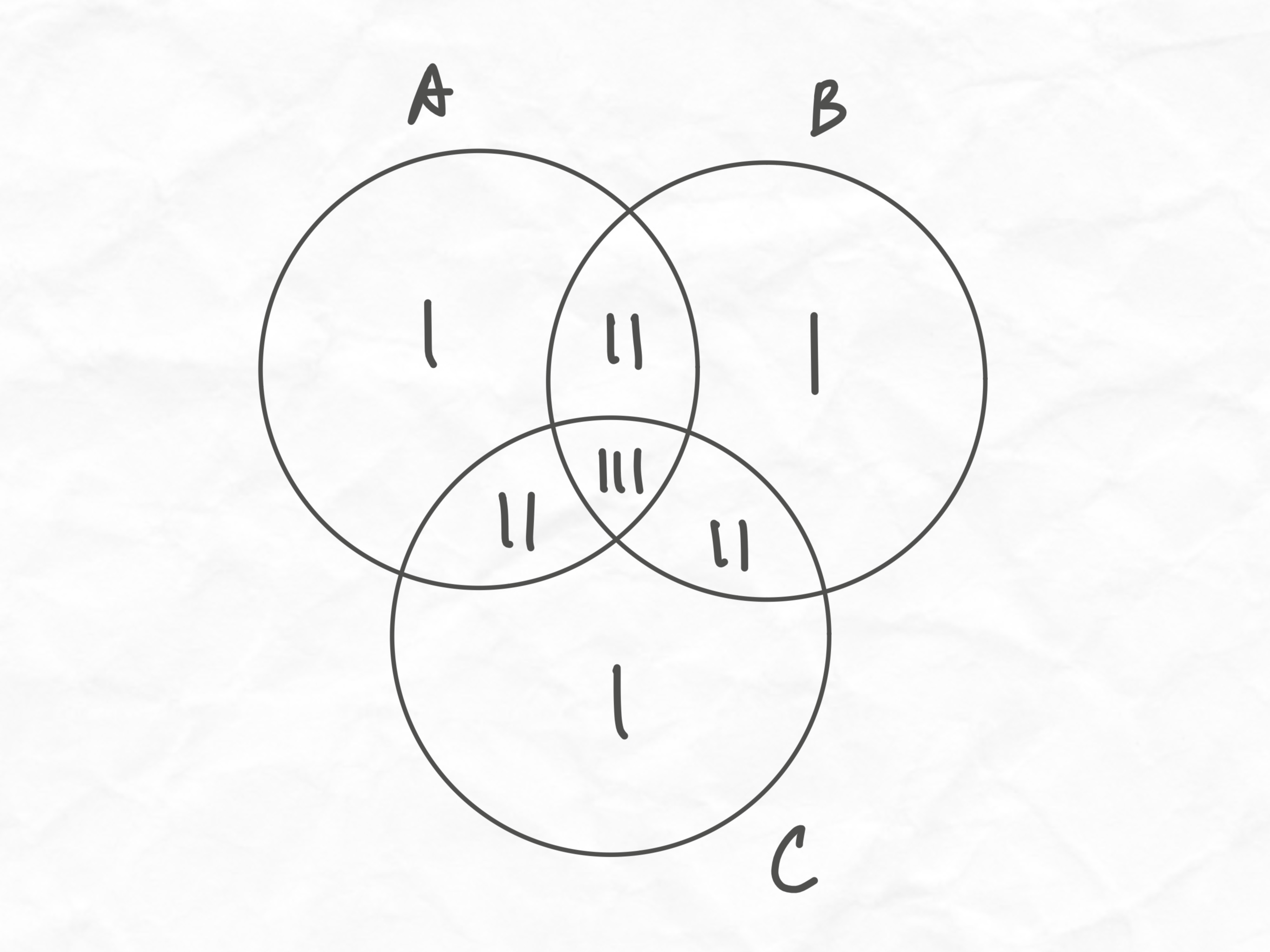
Problems where you use Inclusion-Exclusion

Ex1: Let $S=1,2,3,\cdots ,150.$ Find the number of sets $D$ where $D$ is a set of elements in $S$ that are relatively prime to $70$.

A = divisible by 2 B = divisible by 5 C = divisible by 7

to be solved

Ex2: A random 13 card hand is dealt from a deck of 52 cards. Find the probability that at least one suit is not in the dealt hand.

A = no clubs in hand B = no hearts in hand C = no diamonds in hand D = no spades in hand