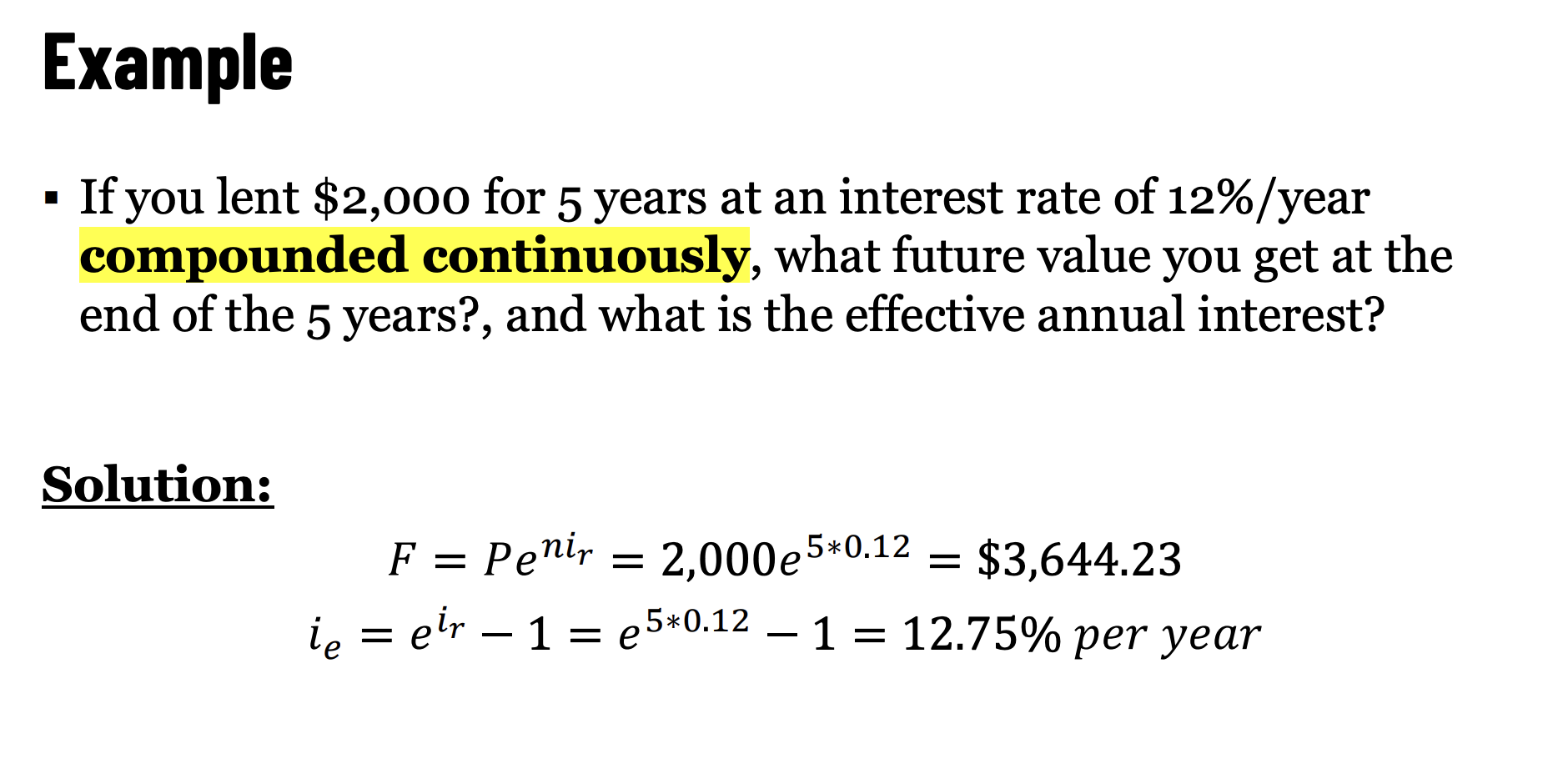Interest Rate

There are two types of interest rates:

1. Simple Interest
2. Compound Interest

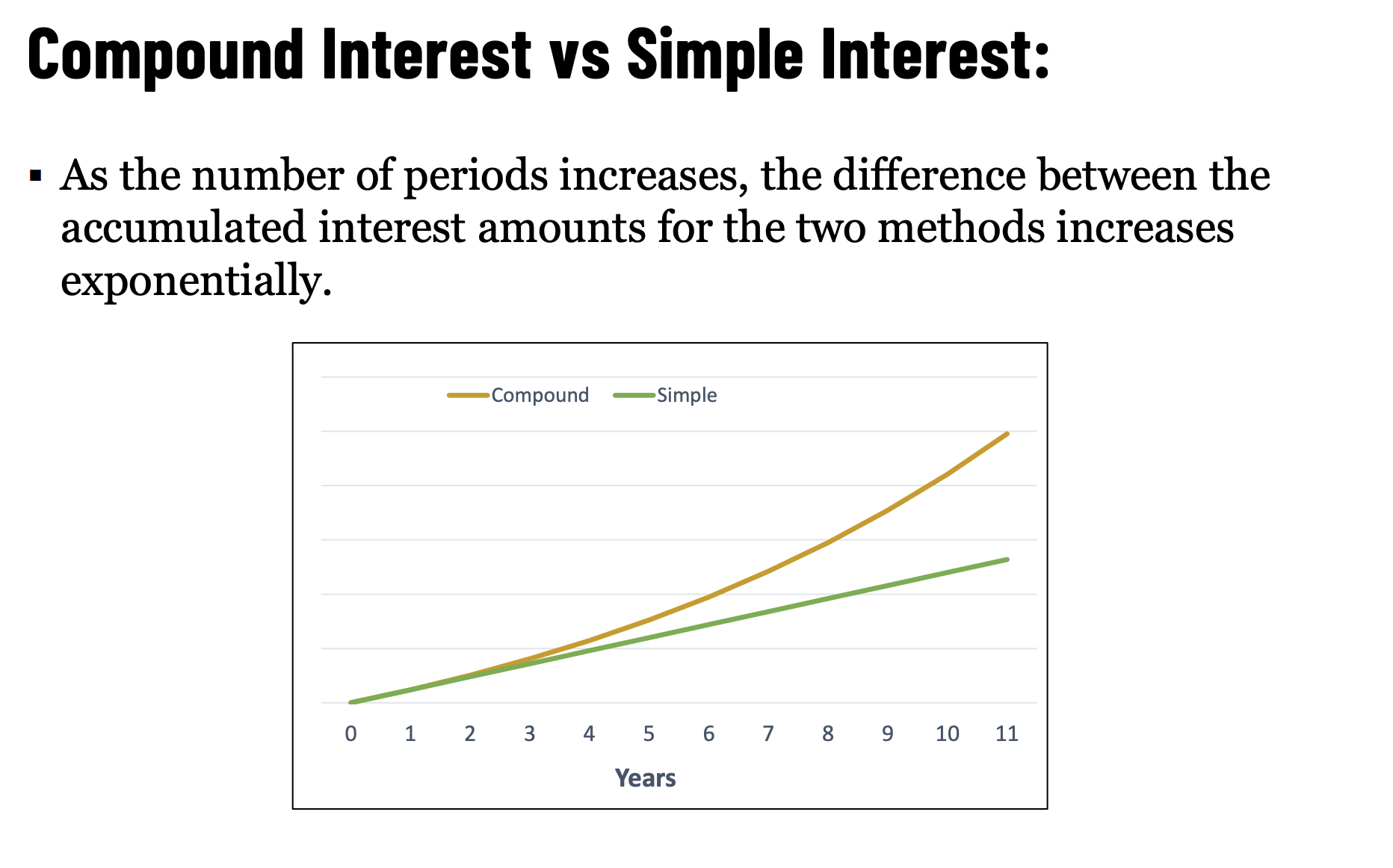
Compound interest is where it’s at, because it is exponential. Compound Effect.

Simple Interest

The following single payment equation applies to simple interest: $F=P(1+in)$ where

• $P$ is the principal (present) amount
• $F$ is the future amount
• $i$ is the simple interest rate, and
• $n$ is the period of time

Compound Interest

The total amount repaid at the end of the $N$ periods is: $F=P(1+i{)}^N$

The total interest on the loan paid at the end of the $N$ periods is: $I_C=P(1+i{)}^N-P$

• $I_C$ is called compound interest

Compound Interest At Banks

If the interest period and compounding period are not stated, then the interest rate is understood to be annual with annual compounding.

Examples:“12% interest” means that the interest rate is 12% per year, compounded annually.

“12% interest compounded monthly” means that the interest rate is 12% per year (not 12% per month), compounded monthly. Thus, the interest rate is 1% (12% / 12) per month.

Nominal Interest Rate

The conventional method for stating the annual interest rate (i.e., it is the annual interest rate not including the effect of any compounding during the year). $i_r=i_s\ast m$

Conversely, $i_s=\frac{i_r}{m}$

Ahh so this is kinda useless? Because it doesn’t actually show how the money compounds.

Effective Interest Rate

The actual interest rate, found by converting a given interest rate with an arbitrary compounding period (less than a year) to an equivalent interest rate with one year compounding period.

$i_e={\left(1+\frac{i_r}{m}\right)}^m-1$

Basically, just look at how much you compound over a given year.

Continuous Compounding

If only this was possible…