Interpolation

Given a set of points, we want to model the general trend of the points by finding a smooth curve that fits the dataset. This is actually what we do in machine learning.

Problem Formulation

Given $p(x_1)=y_1,p(x_2)=y_2,\dots ,p(x_n)=y_n$. estimate $y=p(x)$ for any point $x$ such that $x_1\le x\le x_n$.

CS370

2 ways to go about interpolation:

When there are very few points (<6), we do Polynomial Interpolation

• Vandermonde Matrix (monomial basis)
• Lagrange Form (Interpolation) (lagrange basis)

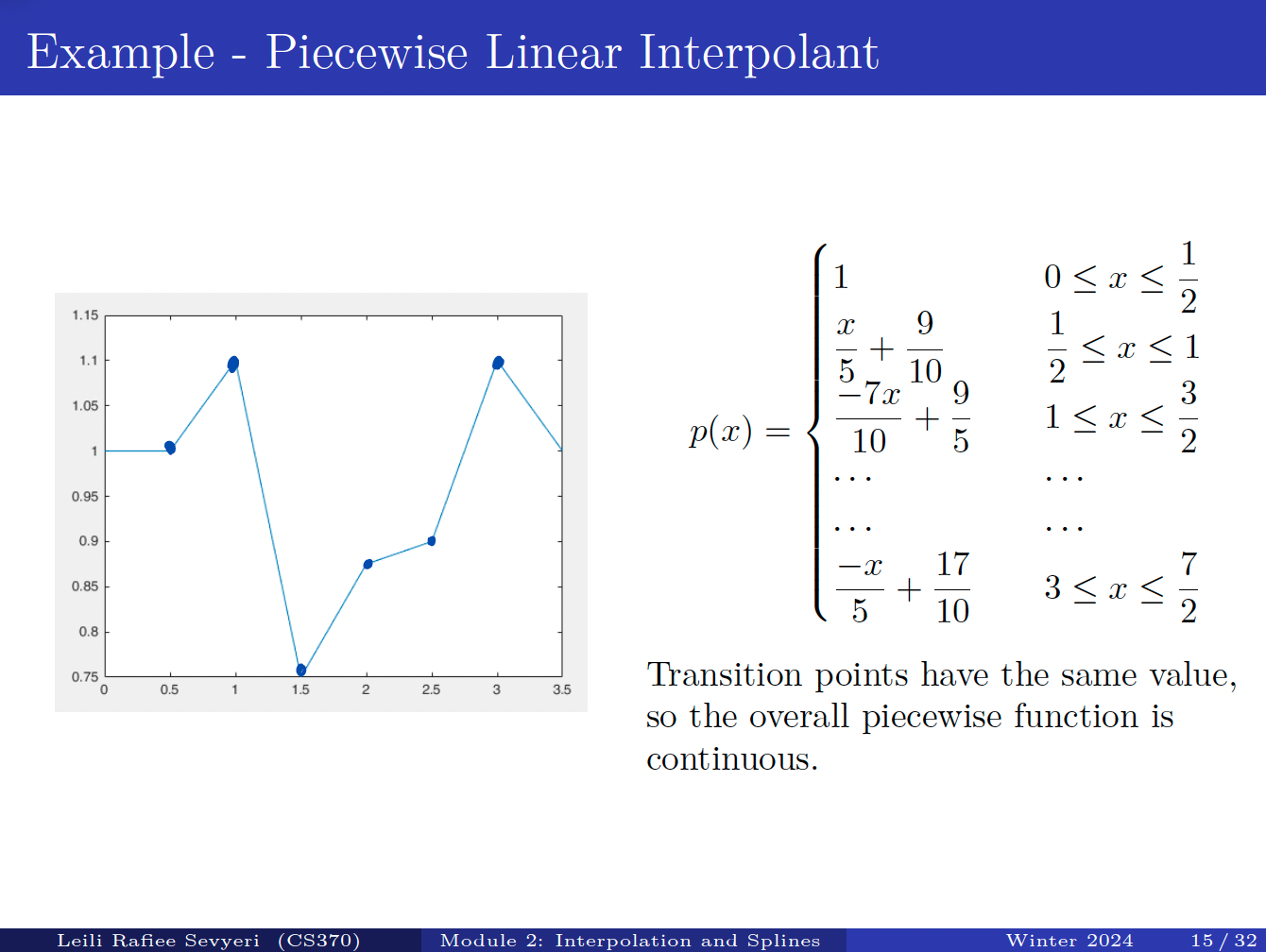
However, then, when there are lots of points, your 1 function might be of degree too high and it won’t be as smooth anymore. Therefore, a better strategy is to use Piecewise Interpolation

• Piecewise linear
• Cubic Spline

There also is another category of interpolation called Hermite Interpolation, where we want to set the derivatives at control points.

Polynomial Interpolation

If we have 5 points, we can find a polynomial of degree 4 passing through these points.

We use the equation below: $y=y_0+x\Delta y_0+x(x-1)\frac{{\Delta }^2{y}_0}{2!}+x(x-1)(x-2)\frac{{\Delta }^3{y}_0}{3!}+\cdots$ $+x(x-1)(x-2)\cdots (x-n+1)\frac{{\Delta }^n{y}_0}{n!}$

Now, it looks very complicated at first, but we can calculate the finite differences very easily. Use the triangular table:

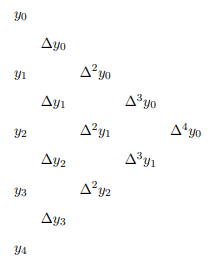
Interpolation in Python

There’s logic for interpolating racing lines.

I need to reference both the TUFTM, and some implementation that the guys at F1TENTH did.

But there’s this Scipy function for interpolation:

class_ scipy.interpolate.interp1d(_x_, _y_, ...)