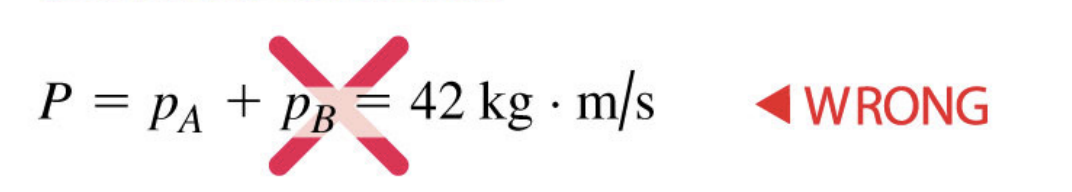Linear Momentum

Linear momentum, $\vec{p}$ is a vector quantity, defined as the product of mass and velocity of an object.

$\vec{p}=m\vec{v}$ ${\vec{F}}_{net}=\frac{d\vec{p}}{dt}$

If mass is constant, we can write $\vec{F}=m\vec{a}$.

→ Momentum is a more fundamental concept than acceleration in physics.

Conservation of Linear Momentum

When the net external force on a system is zero, the total momentum of the system - which is the vector sum of the individual momenta of the constituent particles - remains constant. If ${\vec{F}}_{ext}=0$, then $\frac{d\vec{p}}{dt}=0⟹{\vec{p}}_i={\vec{p}}_f$ $\Delta \vec{p}=0$

Danger

Since momentum is a vector and not a scalar, you cannot simply add up the magnitudes of two momentum.

Defining the right system is important

During a collision between two objects, the force of the collision changes the momentum of each object. Therefore, the momentum of each object is not conserved during the collision, although the total momentum of the two objects is conserved.

Collisions

During an inelastic collision, there is conservation of linear momentum but NO conservation of kinetic energy. The energy is lost in the form of thermal energy, sound, and irreversible deformation of the objects.

During an elastic collision, there is conservation of linear momentum and conservation of kinetic energy.

Elastic Collisions#to-review

We can use the formula below for perfectly elastic collisions. $u^{\prime }=\frac{2m}{m+M}v+\frac{M-m}{m+M}u$ $v^{\prime }=\frac{m-M}{m+M}v+\frac{2M}{m+M}u$

Problem-Solving Strategies

1. Choose a positive direction of the coordinate axis.
2. Define the signs of the initial and final velocities of all moving objects relative to the coordinate axis.
3. Apply Linear momentum conservation law.
4. Apply Energy conservation law (only if collision is perfectly elastic)
   1. This is important and I didn’t really need this in old physics courses. This is needed in many problems

Related

• Impulse
• Rocket Propulsion
• Centre of Mass