Linear Stability

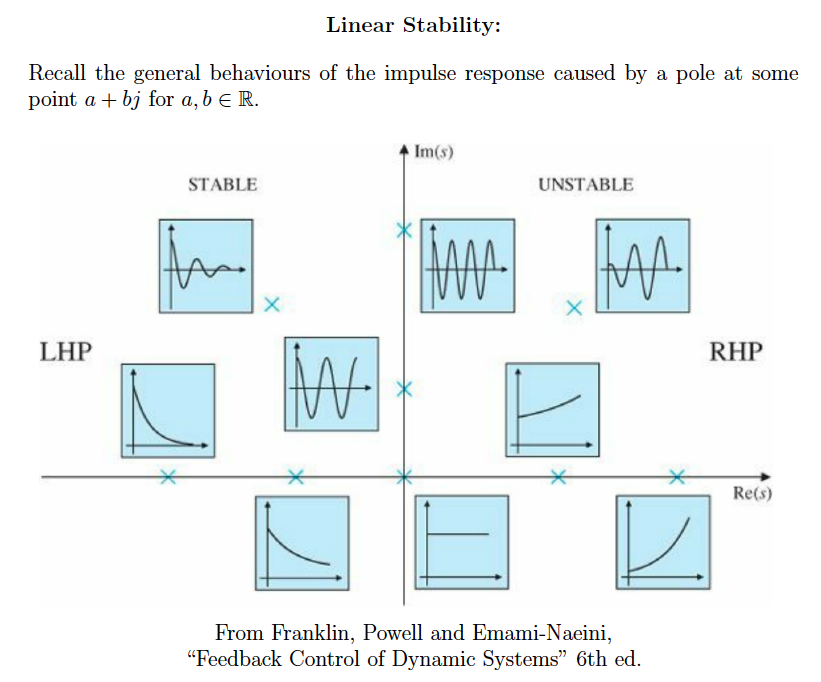
We can look at the stability of a system by looking at the stability of the transfer function!!

Definition 2: System Stability

• LTI, $S$, is stable if $S(\delta (t))$ decays to 0.
• A LTI, $S$, is unstable if $S(\delta (t))$ is unbounded.
• A LTI, $S$ is marginally stable if $S(\delta (t))$ is bounded but does not decay to 0.

Definition 3: Transfer function stability

• A transfer function is stable if the system it is a transfer function for is stable.
• A transfer function is unstable if the system it is a transfer function for is unstable.
• A transfer function is marginally stable if the system it is a transfer function for is marginally stable.

Theorem 1: Stability

A transfer function is stable if all poles have a negative real part.

A transfer function is unstable if there is a pole with a positive real part OR there is a second order pole that has a real part of 0.

A transfer function is marginally stable if there are no poles with positive real parts OR second order poles with a real part of 0 and in addition there is at least order 1 pole that has a real part of 0.

Definition 4: Bounded-input, bounded-output (BIBO) stable

A LTI, $S$, is bounded-input, bounded-output (BIBO) stable if $S(f)$ is bounded for all bounded functions $f$.