Mean Value Theorem
Theorem: If is continuous on and differentiable on , then there exists a number such that
This is easy to forget, so take a look visually:
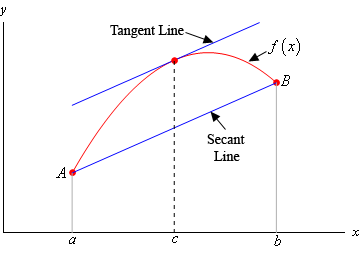
Theorem: If is continuous on and differentiable on , then there exists a number such that
This is easy to forget, so take a look visually:
