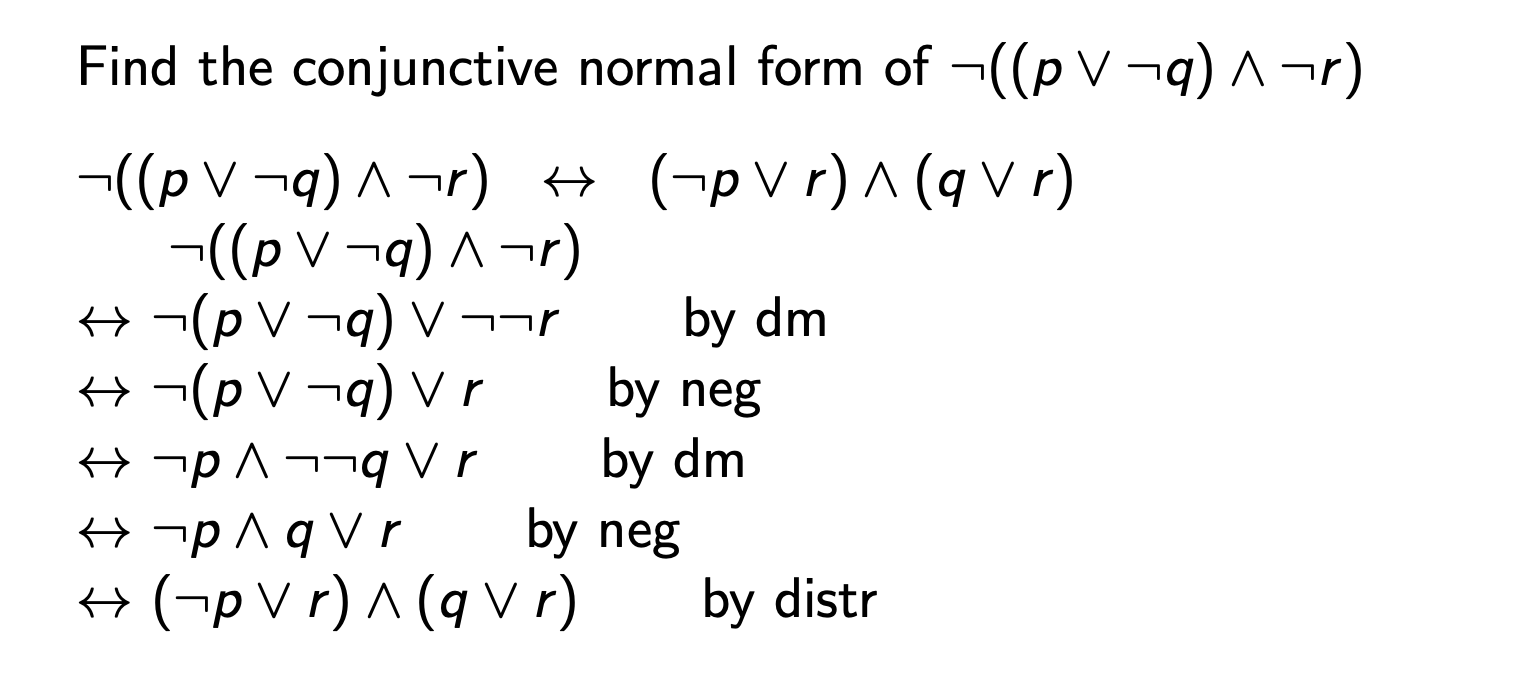Normal Form

Definition. A literal is a proposition symbol or the negation of a proposition symbol.

A formula is in conjunctive normal form (CNF) if it is a conjunction of one or more clauses, where a clause is a disjunction of literals or a single literal.

• Ex: $(\neg p\vee r)\wedge (q\vee r)$

A formula is in disjunctive normal form (DNF) if it is a disjunction of one or more clauses, where a clause is a conjunction of literals or a single literal.

• Ex: $(\neg p\wedge r)\vee (q\wedge r)$

Converting to CNF / DNF

1. Remove all $⟹$ and $⟺$ using impl and equiv laws.
2. If the formula in question contains any negated compound subformulas, either remove the negation by using the negation law or use DM to push the negation in.
3. Once a formula with no negated compound subformulas is found, use the following distributivity laws.
   • For CNF:
     • $A\vee (B\wedge C)\leftrightarrow (A\vee B)\wedge (A\vee C)$
     • $(A\wedge B)\vee C\leftrightarrow (A\vee C)\wedge (B\vee C)$
   • For DNF:
     • $A\wedge (B\vee C)\leftrightarrow (A\wedge B)\vee (A\wedge C)$
     • $(A\vee B)\wedge C\leftrightarrow (A\wedge C)\vee (B\wedge C)$
4. Simplify so there are no repeated literals in a clause and no two clauses with the same set of literals. true, false may appear only if they are the entire formula.

Finding CNF