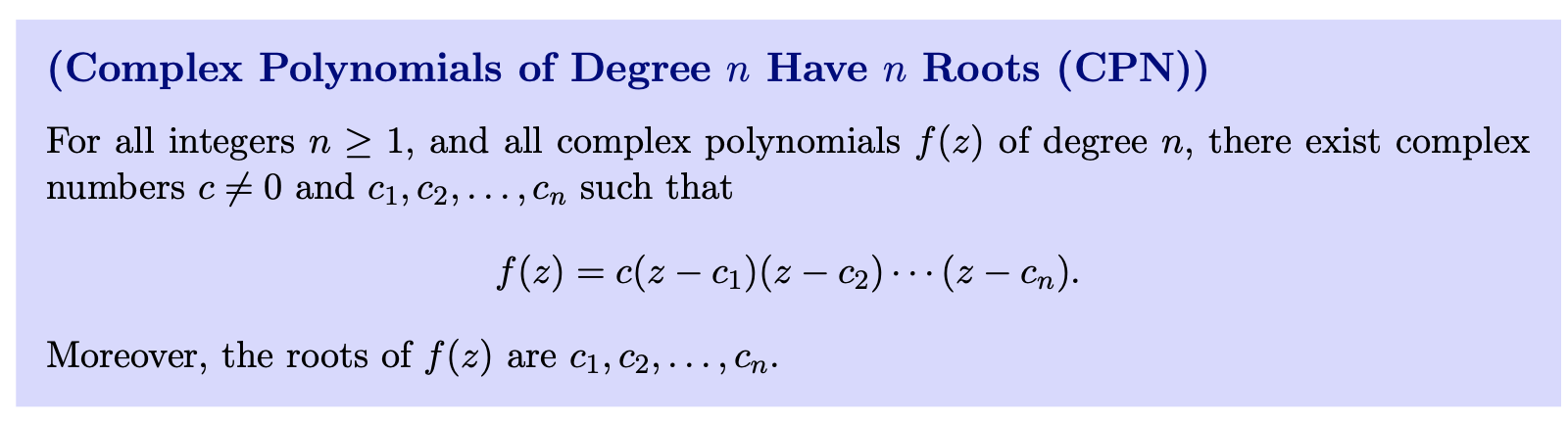Polynomial

Expressions of the form $x^2+2x+1$ are called polynomials.

Notation

The general polynomial in the variable may be written as $P(x)=a_n{x}^n+a_{n-1}{x}^{n-1}+\cdots +a_0$

• The numbers are called coefficients.
• The degree of $P$ is $n$ (assuming that $a_n\ne 0$).
• The coefficient $a_n$ is called the leading coefficient.

We use the notation $\mathbb{R}[x]$ to denote the set of all polynomials with coefficients in $\mathbb{R}$.

Also see Monomial Basis.

Properties

Lemma 1: Degree of a Product (DP) For all non-zero polynomials $f(x)$ and $g(x)$ in $\mathbb{R}[x]$, we have $\mathrm{deg}f(x)g(x)=\mathrm{deg}f(x)+\mathrm{deg}g(x)$

Polynomial Divisibility

Transitivity of Divisibility for Polynomials (TDP) For all polynomials $f(x)$, $g(x)$, $h(x)$ in $\mathbb{R}[x]$, if $f(x)|g(x)$ and $g(x)|h(x)$, then $f(x)|h(x)$.

Divisibility of Polynomial Combinations (DPC) For all polynomials $f(x)$, $g(x)$, $h(x)$ in $\mathbb{R}[x]$, if $f(x)|g(x)$ and $f(x)|h(x)$, then $f(x)|(a(x)g(x)+b(x)h(x))$ for all polynomials $a(x)$, $b(x)$ in $\mathbb{R}[x]$.

Division Algorithm for Polynomials

Division Algorithm for Polynomials (DAP) For all polynomials $f(x)$ and $g(x)$ in $\mathbb{R}[x]$ with $g(x)$ not the zero polynomial, there exist unique polynomials $q(x)$ and $r(x)$ in $\mathbb{R}[x]$ such that $f(x)=q(x)g(x)+r(x)$, where $r(x)$ is the zero polynomial, or $\mathrm{deg}r(x)<\mathrm{deg}g(x)$.

Remainder Theorem (RT) For all polynomials $f(x)\in \mathbb{R}[x]$ and all $c\in \mathbb{R}$, the remainder polynomial when $f(x)$ is divided by $x-c$ is the constant polynomial $f(c)$.

Factor Theorem (FT) For all polynomials $f(x)\in \mathbb{R}[x]$ and all $c\in \mathbb{R}$, the linear polynomial $x-c$ is a factor of the polynomial $f(x)$ if and only if $f(c)=0$ (equivalently, $c$ is a root of the polynomial $f(x)$).

Polynomial Factorization

Factorization Into Irreducible Polynomials (FIIP) Every polynomial in $\mathbb{R}[x]$ of positive degree can be written as a product of irreducible polynomials.