2D Force Representation
3D Force Representation
Steps
- Determine the position vector from TAIL to HEAD of the force, labeled
- Determine the unit vector along the position vector, by dividing each of the components of the position vector by the norm of the position vector
- Determine the force vector, by multiplying the norm (magnitude) of the force by the unit vector
PDF Visual Example
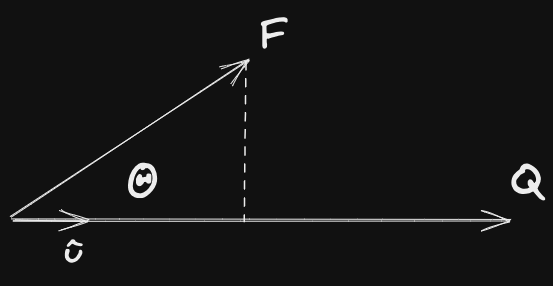
Other method, Use Projections with Dot Product
I really didn’t get this, because I didn’t really understand the dot product well.
By definition, the dot product is
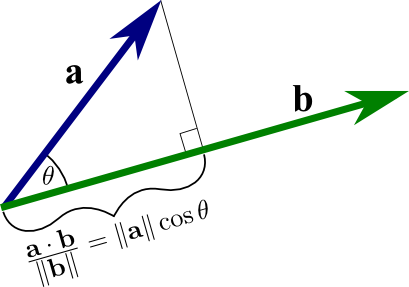 This helped me wrap my head around it
Project Force F in the Q direction.
This helped me wrap my head around it
Project Force F in the Q direction.