Strategic Dominance
Strategic dominance occurs when one strategy is better than another strategy for one player, no matter how that player’s opponents may play. Many simple games can be solved using dominance.
Definitions:
- B is equivalent to A: choosing B always gives the same outcome as choosing A, no matter what the other players do.
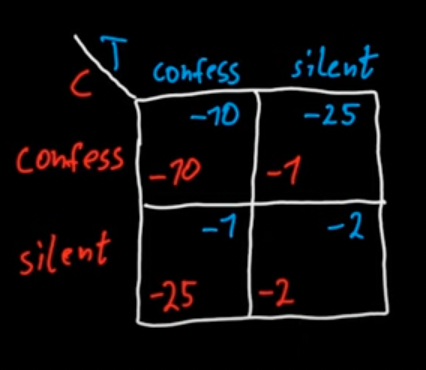
- B strictly dominates A: choosing B always gives a better outcome than choosing A, no matter what the other players do. For example, in the image below
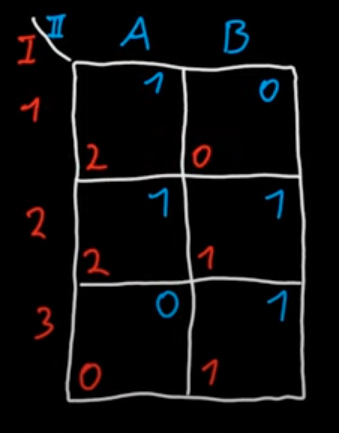
- B weakly dominates A:
- The order of the elimination matters in weak dominance.
- choosing B always gives at least as good an outcome as choosing A, no matter what the other players do, and there is at least one set of opponents’ action for which B gives a better outcome than A. (Notice that if B strictly dominates A, then B weakly dominates A. Therefore, we can say “B dominates A” as synonymous of “B weakly dominates A”.)
- In the example below, we can eliminate a few
- B and A are intransitive: B and A are not equivalent, and B neither dominates, nor is dominated by, A. Choosing A is better in some cases, while choosing B is better in other cases, depending on exactly how the opponent chooses to play. For example, B is “throw rock” while A is “throw scissors” in Rock, Paper, Scissors.