Subgame Solving
https://arxiv.org/pdf/1705.02955.pdf
I found this 1-hour video: https://www.facebook.com/nipsfoundation/videos/1553539891403911/
Good background
The key problem that you need to understand is that unlike Perfect Information games where you can solve subgames in isolation, in Imperfect Information you cannot do that.
^I think the above is confusing.
“In perfect-information games, determining the optimal strategy at a decision point only requires knowledge of the game tree’s current node and the remaining game tree beyond that node (the subgame rooted at that node). This fact has been leveraged by nearly every AI for perfect information games.” Noam Brown thesis
In chess for example, I can give you a chess state, and you can just solve your way downwards. Previous decisions don’t matter.
In Poker, that matters. How you ended up in that state matters.
What do we mean by "Solving"?
“Solving” a subgame refers to finding the optimal strategy for that subgame. We do this by calculating the Expected Value of the subgame:
expected value = payoffs for each outcome * probability of outcome occurring
The optimal strategy is then action that maximizes the expected value of the subgame.
Attempting to understand this again
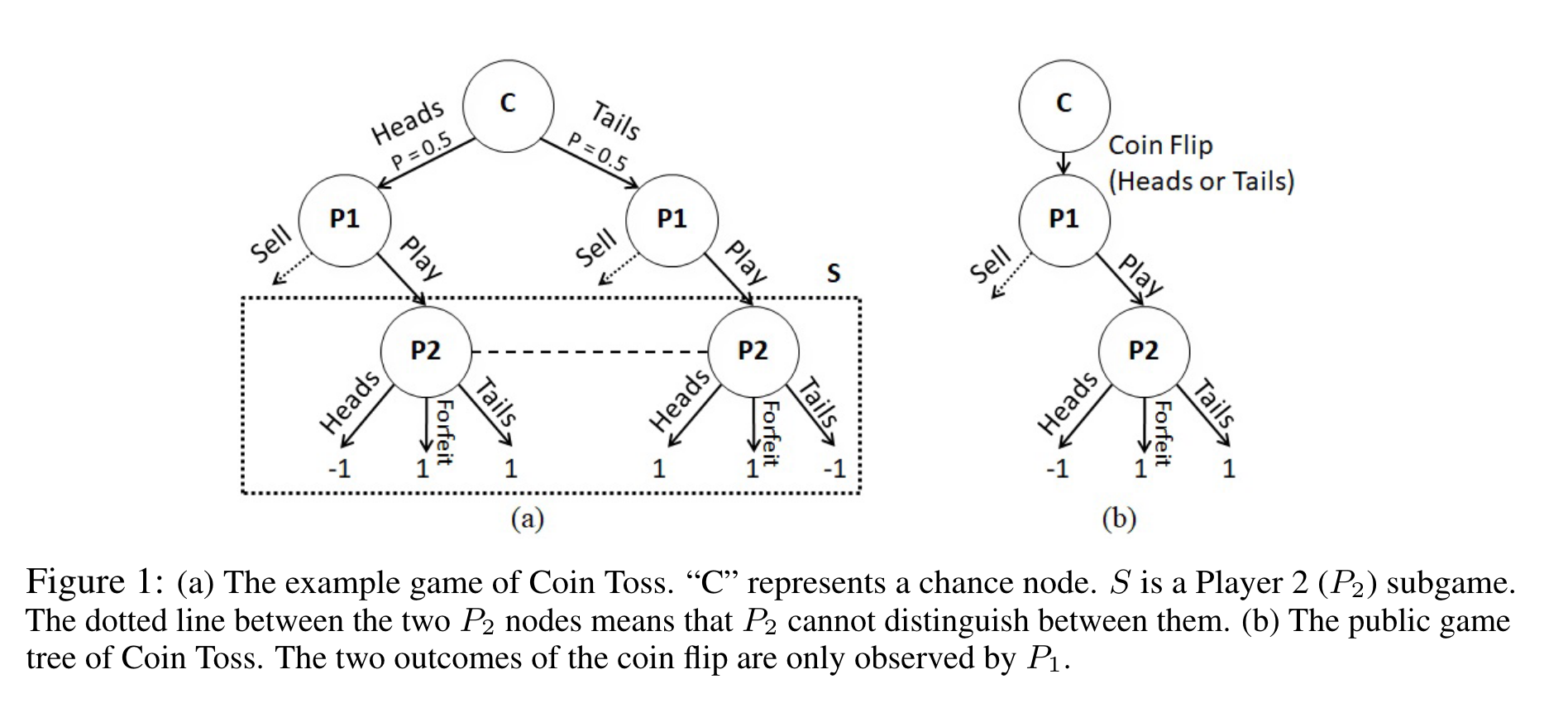
- P1 tosses the coin for heads or tail
- P2 tries to guess heads or tail
Assume this is our blueprint strategy profile, we want to apply subgame solving
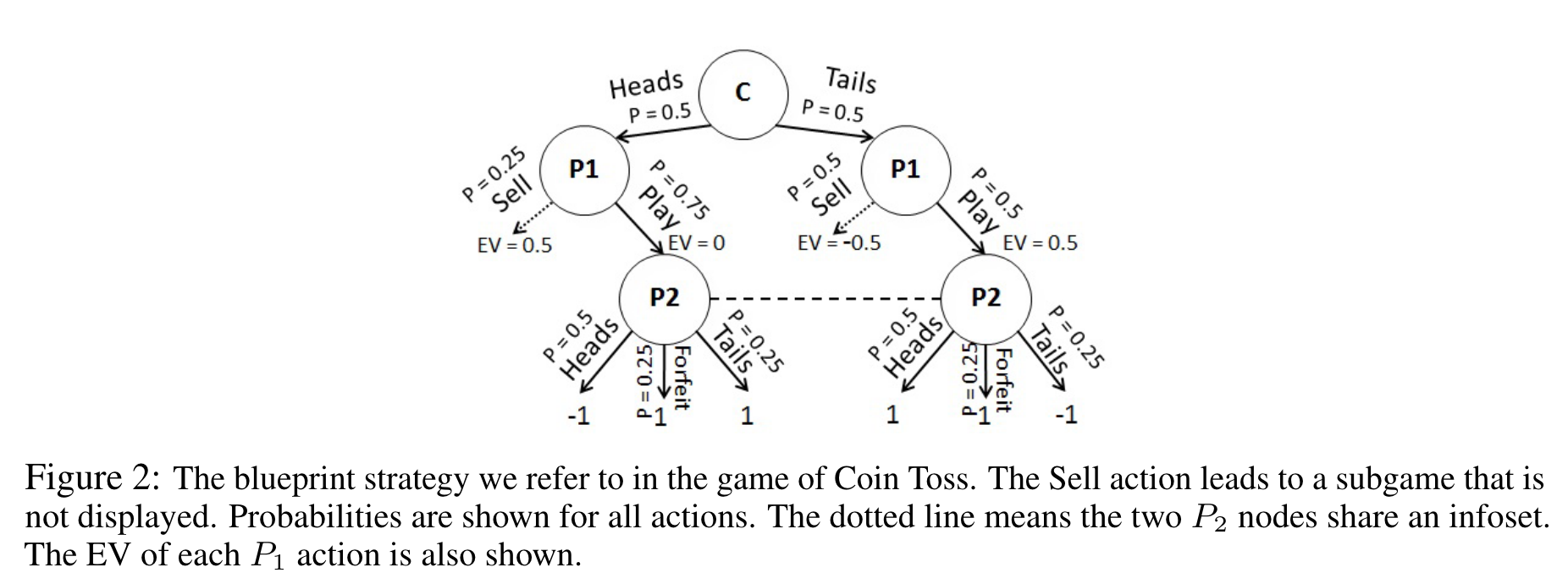
We assume that P1 plays according to the nash equilibrium. Then, we can infer the probability of the coins being heads or tails. And so we can run CFR on this local subgame.
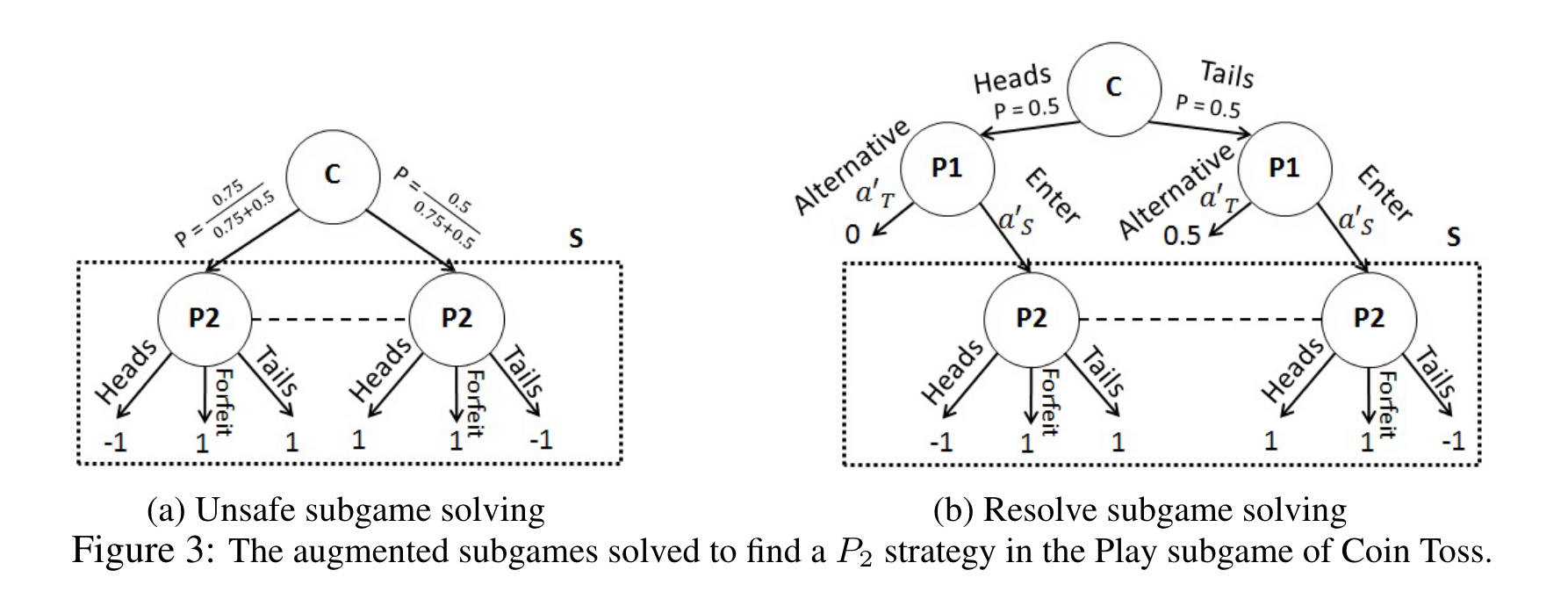
And so we can run CFR on this local subgame, and get a new strategy for this subgame
- I guess you start from the chance node,
Reach subgame solving introduces this idea that we must be aware of other subgames.
- And then this idea of gifts
Nested subgame solving is applying reach subgame solving to Poker, by enabling reactions off-game-tree actions.
The Problem (I dont understand this tbh)
What Noam Brown is pointing out is the fact that a state can have multiple expected values, depending on the opponent’s strategy, and the payouts in other subgames. This is what makes imperfect information games hard.
- Noam Brown talks about how to avoid this issue, they just solve until the end of the game, but this is not feasible
I can maybe implement a strategy that does unsafe search, which leads to higher Exploitability, but no, one should be reasoning to play more optimally.
I think this makes it clear: A player’s optimal strategy in a subgame can depend on the strategies and outcomes in other parts of the game. Thus, one cannot solve a subgame using information about that subgame alone.
So depending on what kind of hidden payoffs a player has, the optimal strategy differs.
If coin lands heads and we sell, we get 0.50 EV
- Imagine there is a subgame going on after sell, and that optimal play from there results in X expected value. We are going to illustrate that this will affect the strategy of the current subgame!! I FINALLY GET IT!
P2 Optimal Strategy: Tails with 75% probability and Heads with 25% probability
However, if the selling rewards are flipped, i.e. selling heads is −0.50, then P2’s optimal strategy: Heads with 75% probability and Tails with 25% probability
So a particular subgame can affect the optimal strategy for a subgame.
For RPS, imagine the case that you have 2x payout for the winner if either player plays scissors. Then more of the time do you want to play scissors.
So the existence of hidden utilities, people’s personal rewards that we don’t know, that is the difficulty in Imperfect Information games??
I think this is because of the existence of Information Sets, because two different scenarios are seen as the same for the opponent and for you. So other ways opponents play affect this particular solution.
In Imperfect Information games, you can just solve the subgame in isolation, but even in a game like RPS, you can’t really do that.
They illustrate this through the coin toss example. So there is the existence of chance events.
In the above coin toss example, a rundown of my algorithm, first computing P2 BR, we would try either heads, tails or forfeit. Assume our opponent plays some sort of strategy profile, then P2 plays a deterministic strategy. In this case, only one Information Set for the opponent, so P2 would only play that.
Then, we might find that playing tails all the time is best for . So implementing Depth-LImited Solving, we add that to a set of strategies.
The question is, how does now take that into consideration?