Time-Stepping Methods

Was introduced to this in CS370.

Time-stepping applies a Recurrence Relation to approximate the function values at later and later times.

• Given $y_0$, approximate $y_1$. Given $y_1$, approximate $y_2$. etc.

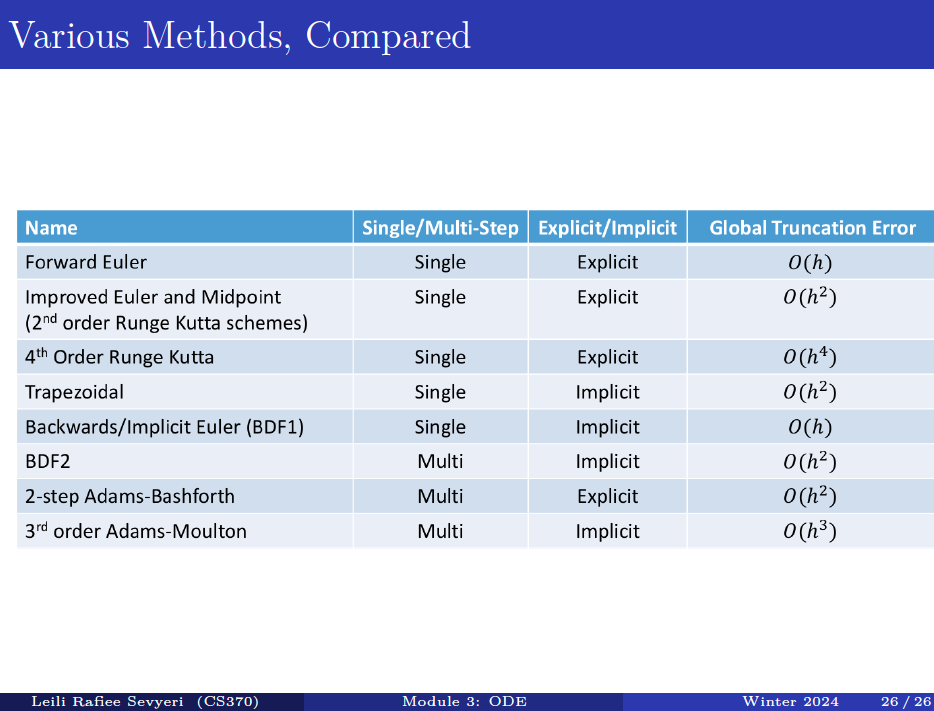
There are several varieties/categories of time-stepping methods:

• Single-step vs. Multistep: do we use information only from the current time, or from previous timesteps too?
• Explicit vs. Implicit: Is $y_{n+1}$ given as an explicit function to evaluate, or do we need to solve an implicit equation?
• Timestep size: Do we use a constant timestep $h$, or allow it to vary?

Methods:

• Forward Euler Method (explicit, single step)
• Trapezoidal Rule (implicit)
• Improved Forward Euler (explicit)
• Backward Euler
• Runge-Kutta Method
• Backwards Differentiation Formula (multi-step)

Implicit vs. Explicit Function

e.g., given $x$ and $z$, determine $y$. Explicit function ($y$ only on one side): $y(x,z)=2x^2+\sqrt{\log (z)}$

• Easy – just evaluate

Implicit function ($y$ on both sides): $y=x^3+17z{x}^2+\sin (\sqrt{y})$

• Harder – requires solving

Explicit vs. Implicit schemes

Explicit vs. Implicit Schemes

Explicit:

• Simpler, and fast to compute per step.
• Less stable – require smaller timesteps to avoid “blowing up”. (More later!)

Implicit:

• Often more complex and expensive to solve per step.
• More stable – can safely use larger timesteps.