Trigonometric Function
Consider the unit circle, . We have
See Trigonometric Identities for useful properties.
Working with Sines and Cosines
In some applications of calculus to physics and engineering, we’ll have input information of the form but we’ll find that our mathematical analysis will result in output of the form We use the [[notes/Trigonometric Identities#Sum and Difference Formulas|Trigonometric Identities#Sum and Difference Formulas]] to equate the two and solve for and .
title:
See [[Simple Harmonic Motion]] for working with sinusoidal functions with the period and amplitude.Also see Euler’s Formula to write sin and cos in terms of complex exponentials.
Inverse Trigonometric Functions
Inverse trig functions don’t actually exist, since no periodic function can have an inverse (because periodic functions can’t be one-to-one). Inverse trig functions are inverses of versions of the trigonometric functions which have restrictions imposed on their domains.
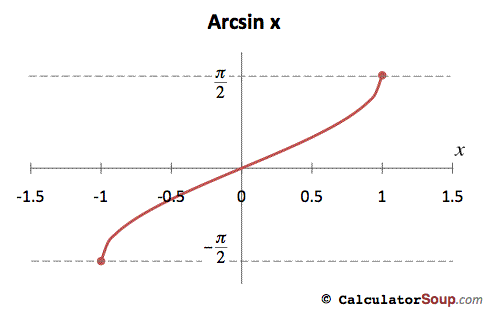
Inverse Sine Function
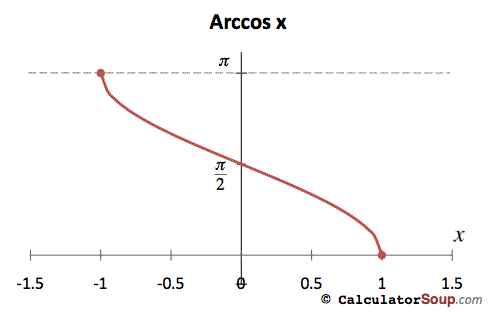
 Inverse Cosine Function
Inverse Cosine Function
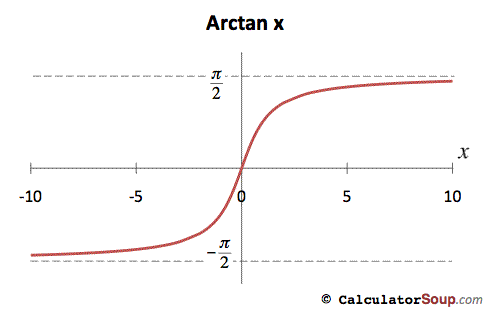
 Inverse Tangent Function
Inverse Tangent Function