Offline Reinforcement Learning with Implicit Q-Learning (IQL)

In this work, we primarily consider the Implicit Q-Learning (IQL) [20] value objectives given its effectiveness on a range of tasks. IQL aims to fit a value function by estimating expectiles τ with respect to actions within the support of the data, and then uses the value function to update the

Q-function. To do so, it aims to minimize the following objectives for learning a parameterized Q-function $Q_{\varphi }$ (with target Q-function $Q_{\hat{\theta }}$ ) and value function $V_{\psi }$: $L_Q(\varphi )=E_{(s,a,r,s^{\prime })\sim D}[(r+\gamma V_{\psi }(s^{\prime })-Q_{\varphi }(s,a){)}^2]$ L_V (ψ) = E_{(s,a)∼D} [L^τ_2 (Q_\widehat{\theta} (s, a) − V_ψ(s))]

• where $L_2^{\tau }(x)=|\tau -1(x<0)|x^2$.
• The target Q_\widehat\theta is a delayed version of $Q_{\theta }$ via Polyak Averaging

For the policy, use AWR

L_\pi(\phi) = \mathbb{E}_{(s,a) \sim D} \left[ e^{\beta (Q_\widehat\theta(s,a) - V_\psi(s))} \log \pi_\phi(a|s) \right]

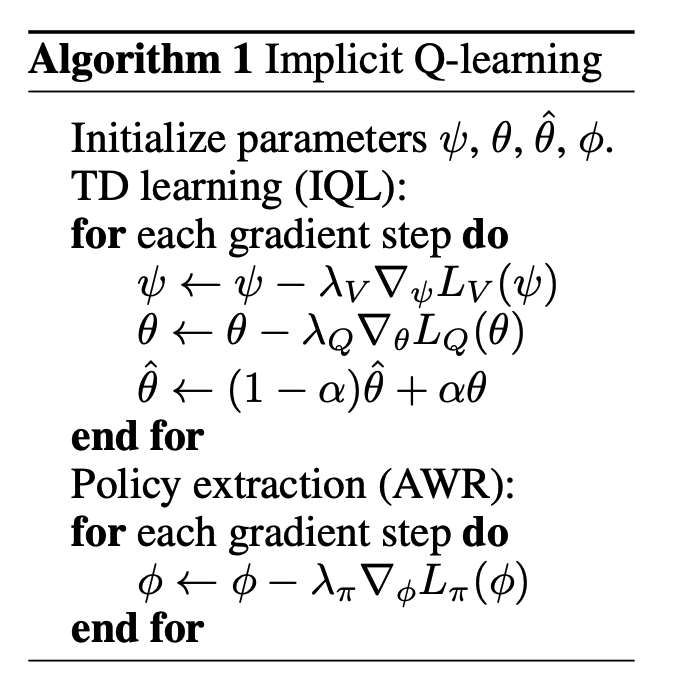
It learns a Q-function from the offline dataset.

It derives a value function $V(s)$ by “aggregating” the learned Q-function across actions.

It then trains the policy to imitate the best actions in the dataset (using advantage-weighted updates).