Alpha-Beta Pruning
http://www.cs.toronto.edu/~hojjat/384f06/Lectures/Lecture06-4up.pdf
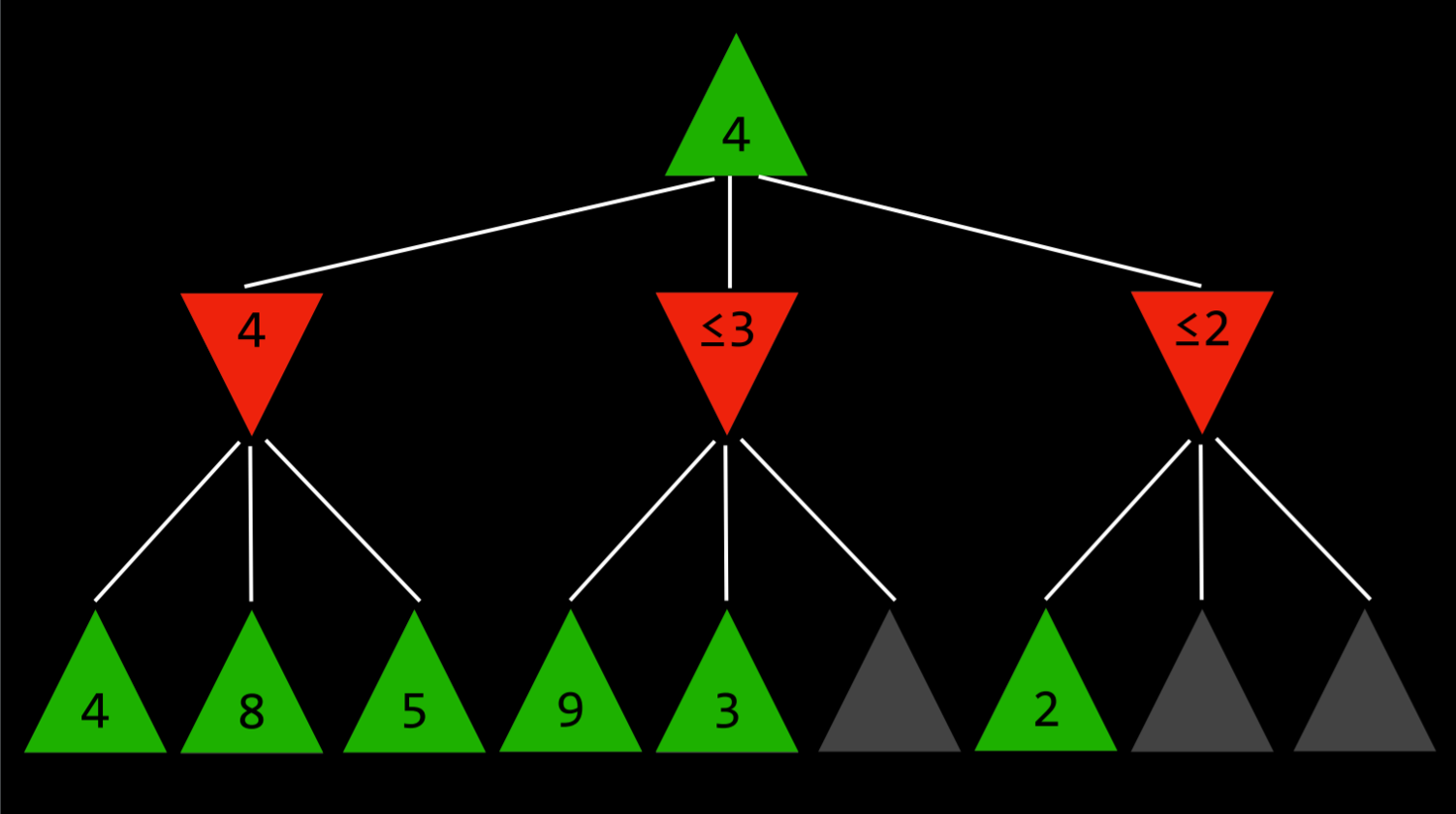
A way to optimize Minimax, Alpha-Beta Pruning skips some of the recursive computations that are decidedly unfavourable.
The benefit of alpha–beta pruning lies in the fact that branches of the search tree can be eliminated. This way, the search time can be limited to the ‘more promising’ subtree, and a deeper search can be performed in the same time.
One big problem: Assumes the opponent is rational
Pseudocode
Minimax with Alpha-Beta Pruning. Recursive calls.
def minimax(state, max_depth, is_player_minimizer, alpha, beta):
if max_depth == 0 or state.is_end_state():
return evaluation_function(state)
if is_player_minimizer:
value = -math.inf
for move in state.possible_moves():
evaluation = minimax(move, max_depth - 1, False, alpha , beta)
min = min(value, evaluation)
# Keeping track of our current best score
beta = min(beta, evaluation)
if beta <= alpha:
break
return value
value = math.inf
for move in state.possible_moves():
evaluation = minimax(move, max_depth - 1, True, alpha, beta)
max = max(value, evaluation)
# Keeping track of our current best score
alpha = max(alpha, evaluation)
if beta <= alpha:
break
return value