Ampere’s Law

We just need a closed loop. We don’t need a closed surface like we needed to apply Gauss Law. ${\oint }_C\vec{B}\cdot d\vec{l}={\mu }_0{I}_{enc}={\mu }_0{\int }_S\vec{J}\cdot d\vec{S}$

Use the right hand rule and curl your fingers around the loop. Your thumb will be pointing in the positive current direction.

You can definitely make a parallel to Gauss Law. Same thing with $Q_{encl}$ but for $I_{encl}$

Calculations Steps to find Magnetic Field

Making parallels with Gauss Law to find Electric Field, but Ampere’s Law is much less strict. → Ex: See how it is used in Solenoid?

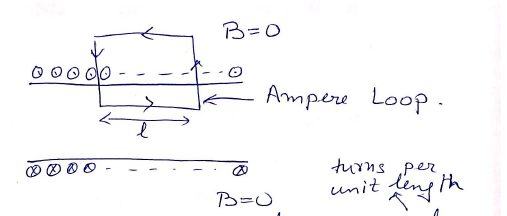
We need to remember that the loop is a 2D structure. So we have to see how current is flowing to take a cross-section perpendicular to the current. On this plane, we look for symmetry and think of a loop where $\vec{B}$ would be constant.

Steps

1. Identify symmetry, sketch magnetic field lines
2. Draw or define a proper Amperian loop to evaluate $\oint \vec{B}\cdot d\vec{l}$
   1. Make sure that $\vec{B}$ is always parallel or perpendicular to $d\vec{l}$ so that you can factor $\vec{B}$ out
3. Rearrange and solve for $|\vec{B}|$
4. Determine the direction of $\vec{B}$ in final answer

Practical application: use of a Clamp Meter