Banker’s Algorithm

Consider a system of $n$ processes and $m$ different types of resources. We define the following vectors and matrices:

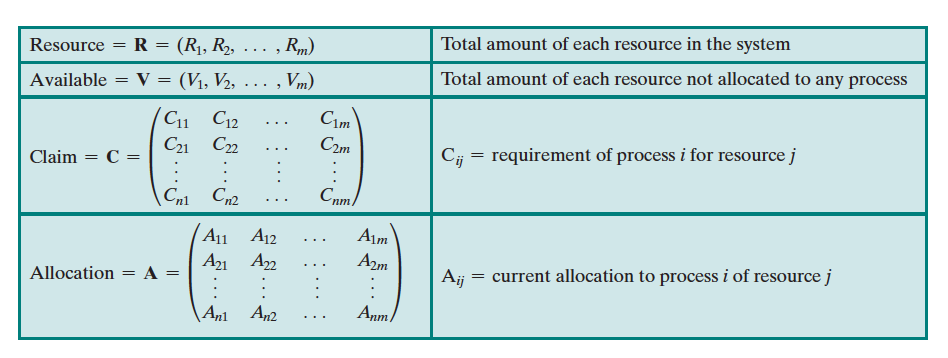
Furthermore, the following relationships hold:

1. $R_j=V_j+{\sum }_{i=1}^n{A}_{ij}$, for all $j$
   • All resources are either available or allocated.
2. $C_{ij}\le R_j$, for all $i,j$
   • No process can claim more than the total amount of resources in the system.
3. $A_{ij}\le C_{ij}$, for all $i,j$
   • No process is allocated more resources of any type than the process originally claimed to need

The state of the system reflects the current allocation of resources to processes. Consists of:

• 2 vectors: Resource and Available
• 2 matrices: Claim and Allocation

We define 2 kinds of states:

• Safe state is where there is at least one sequence that does not result in deadlock
• Unsafe state is a state that is not safe

The goal is to always have a safe state.

How to compute?

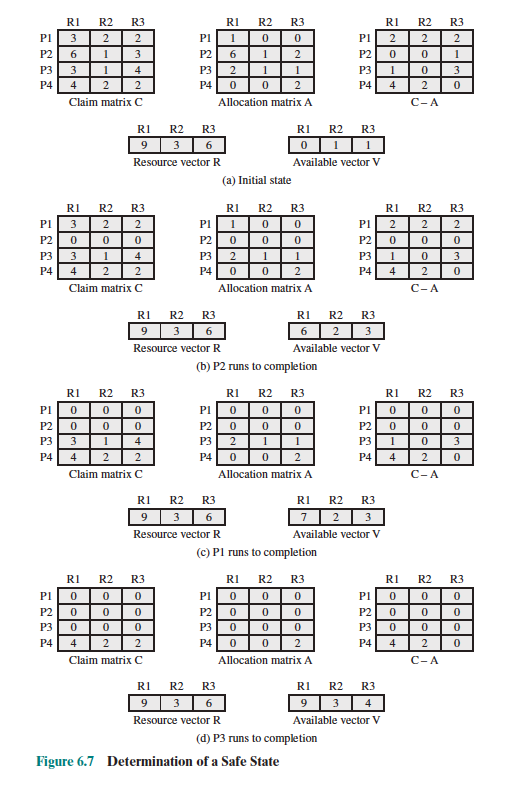
As yourself, is this a safe state? To figure this out, ask yourself, the very simple question:

• can any one of the four processes be run to completion with the resources available?

In the example:

• No possible for P1, which needs 2 more units of R1, but there are 0 R1 units left.
• Possible for P2.

So then, you run P2 to completion, and then the resources are freed. You continually ask the question, and if you manage to run all 4 processes to completion, you figure out that the initial state is a safe state.

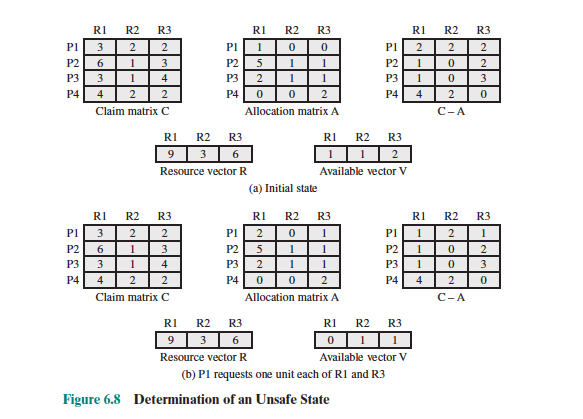
In this new example, none of the processes can be run to completion. Not enough resources.

Pseudocode

Example code from p.305 of SE350 textbook

Global Data Structures

struct state {
    int resource[m];
    int available[m];
    int claim[n][m];
    int alloc[n][m];
}

Resource allocation algorithm

if (alloc [i,*] + request [*] > claim [i,*])
    <error>; /* total request > claim*/
else if (request [*] > available [*])
    <suspend process>;
else { /* simulate alloc */
    <define newstate by:
    alloc [i,*] = alloc [i,*] + request [*];
    available [*] = available [*] - request [*]>;
}
if (safe (newstate))
    <carry out allocation>;
else {
    <restore original state>;
    <suspend process>;
}

Test for safety algorithm (banker’s algorithm)

boolean safe (state S) {
    int currentavail[m];
    process rest[<number of processes>];
    currentavail = available;
    rest = {all processes};
    possible = true;
    while (possible) {
        <find a process Pk in rest such that
        claim [k,*] – alloc [k,*]<= currentavail;
        if (found) { /* simulate execution of Pk */
            currentavail = currentavail + alloc [k,*];
            rest = rest - {Pk};
    }
    else possible = false;
    }
    return (rest == null);
}