Image Interpolation

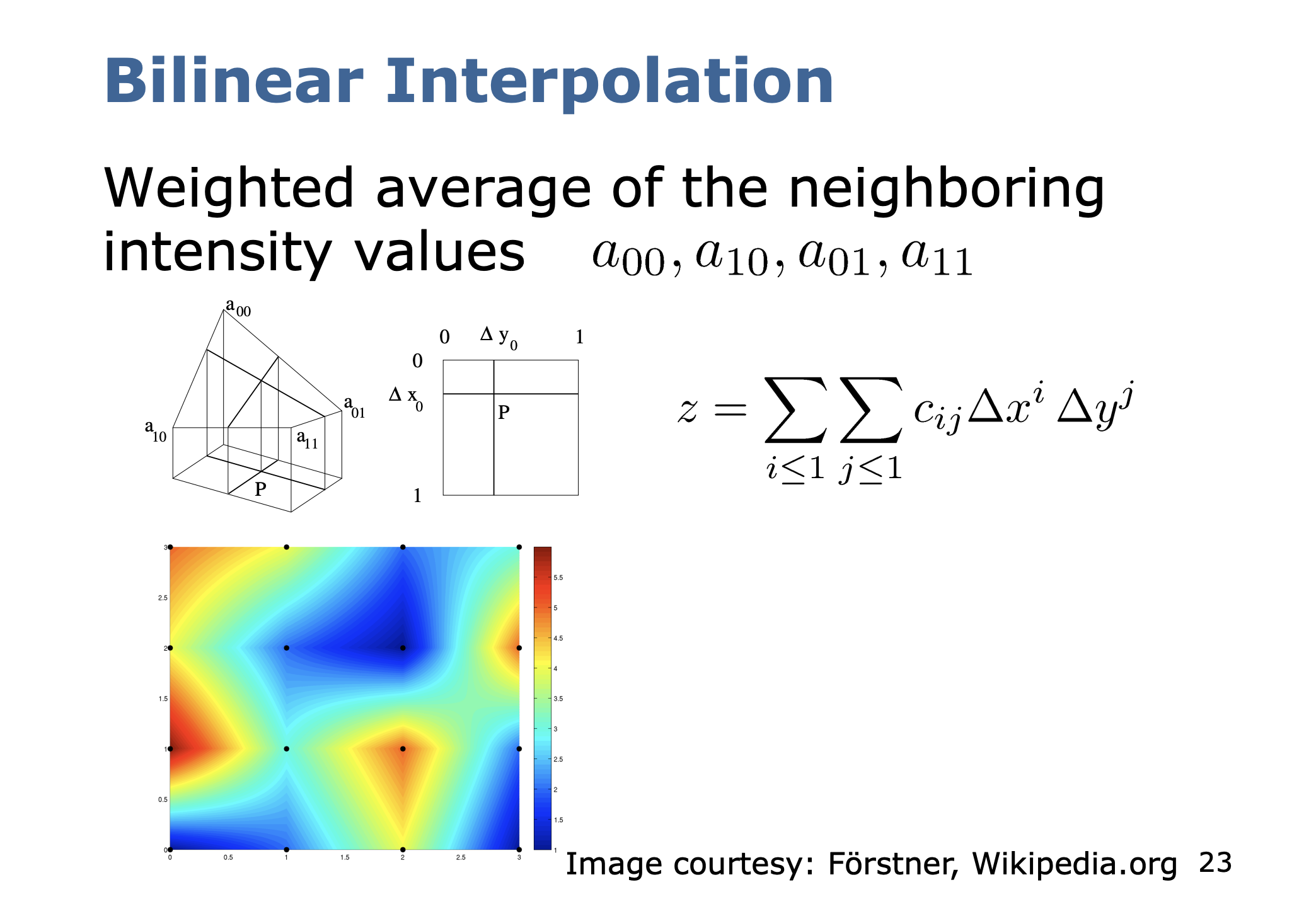
Bilinear Interpolation

Heard Jack Zhang from NVIDIA say this term while he was working on ESS.

Resources

• https://theailearner.com/2018/12/29/image-processing-bilinear-interpolation/

notes from Cyrill Stachniss.

Bilinear Interpolation

This is intuitive. To calculate the new intensity value, compute a weighted average of the 4 neighbouring pixel intensity values.

\begin{align} b(x,y) = &a_{00} (1- \Delta x)(1- \Delta y) + a_{01}(1-\Delta x)\Delta y \\ &+ a_{10} \Delta x (1 - \Delta y) + a_{11} \Delta x \Delta y \end{align}

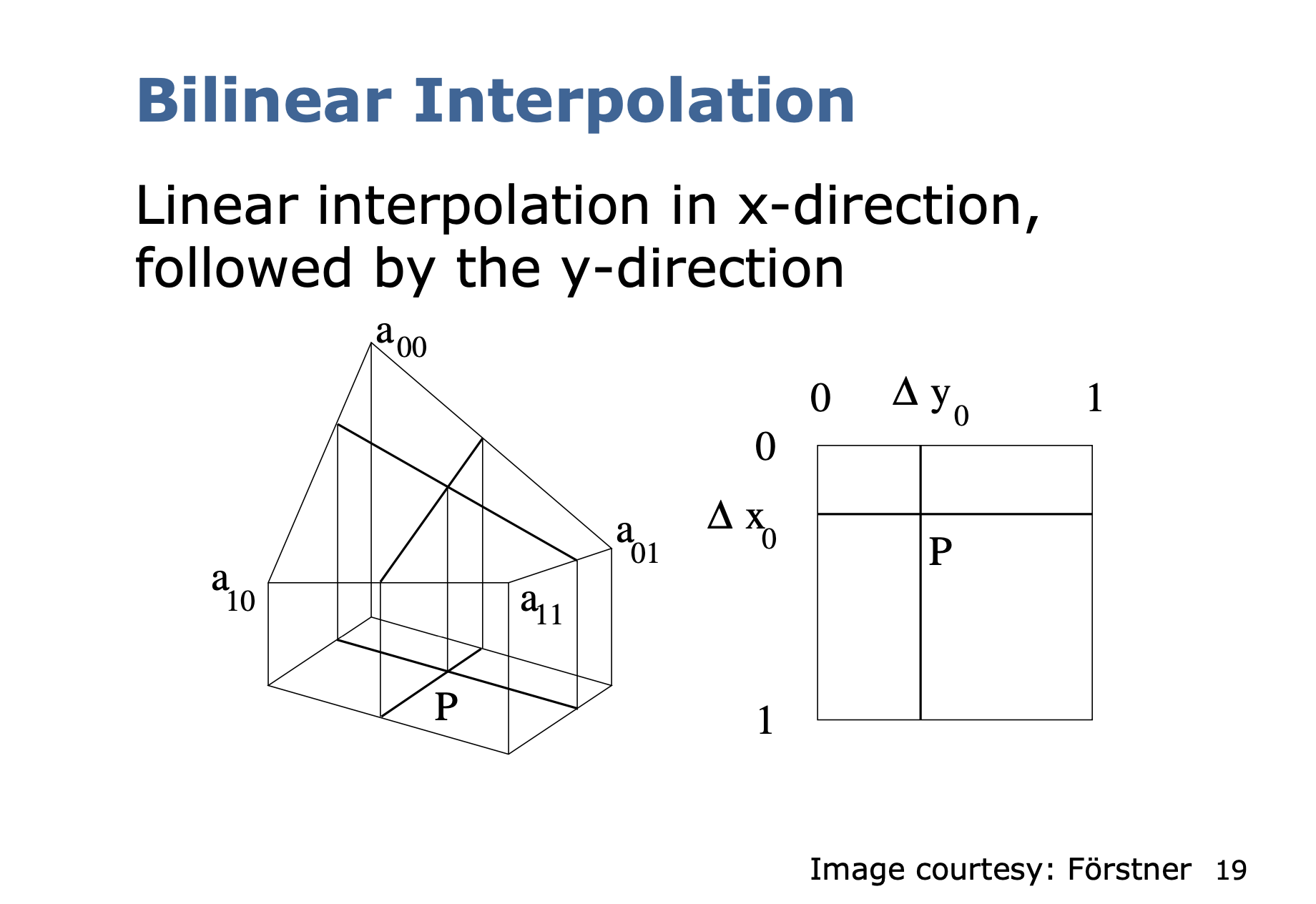
• Where $a_{00},\dots a_{11}$ are the 4 neighbouring pixel intensity values

Normalized

Notice that things seem to be normalized between 0 and 1 here. I don’t know how I am supposed to do this in practice.

Cyrill Stachniss likes to write this more compact form

$z={\sum }_{i\le 1}{\sum }_{j\le 1}{c}_{ij}\Delta x^i\Delta y^j$

However, be careful since $c_{ij}$ doesn’t correspond to $a_{ij}$.

How am I supposed to determine c_{ij}?

You need to compare the original equation term by term.

c_{01} &= a_{01} - a_{00} \\ c_{10} &= a_{10} - a_{00} \\ c_{11} &= a_{11} - a_{10} - a_{01} + a_{00} \\ \end{align}$$ ![[attachments/Screenshot 2023-10-08 at 1.38.46 PM.png]]