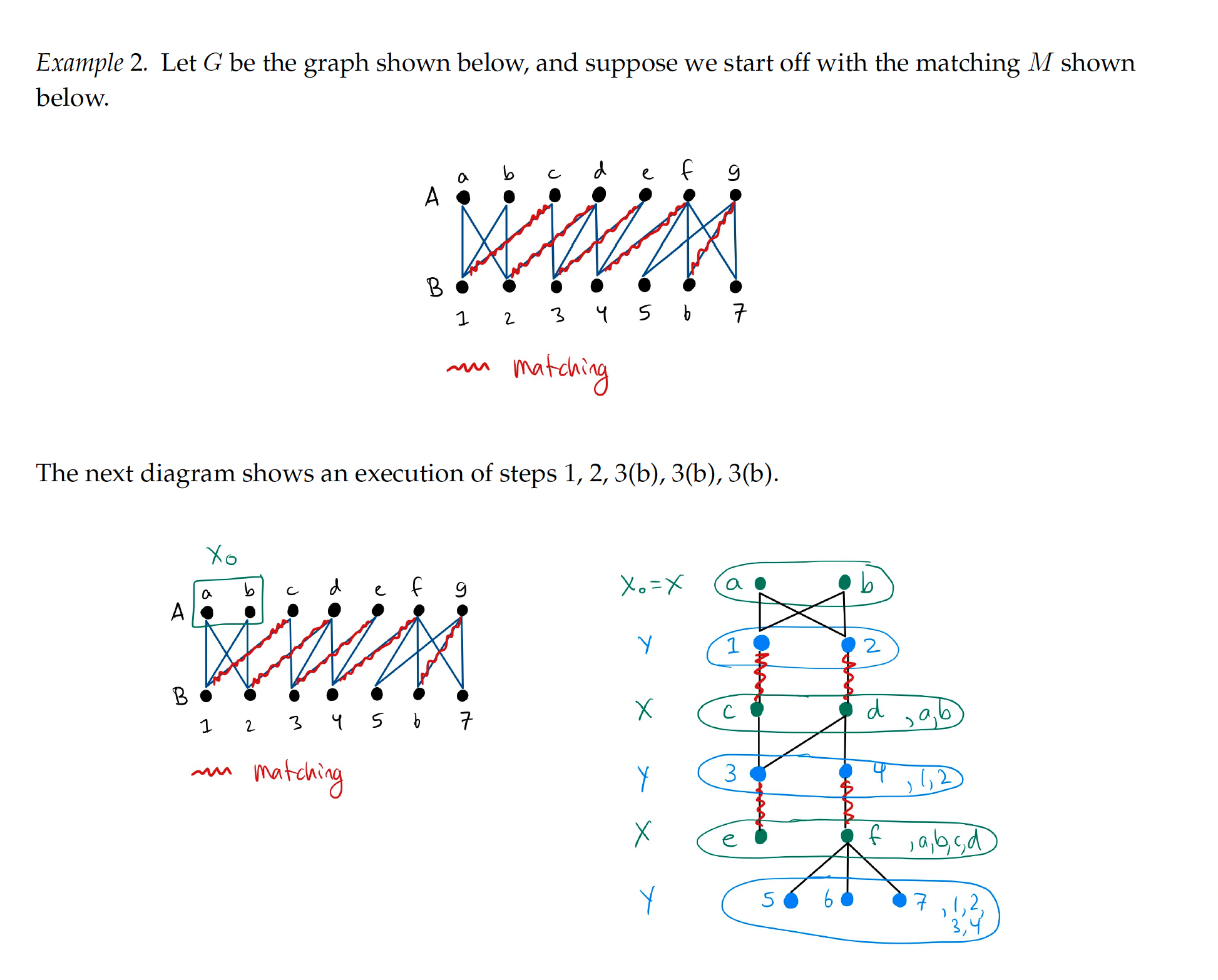
Bipartite Matching Algorithm

This is an algorithm which looks for augmenting paths, used to prove Konig’s Theorem.

Pseudocode

Given a bipartite graph $G$ with bipartition $(A,B)$, and a matching $M$ of $G$.

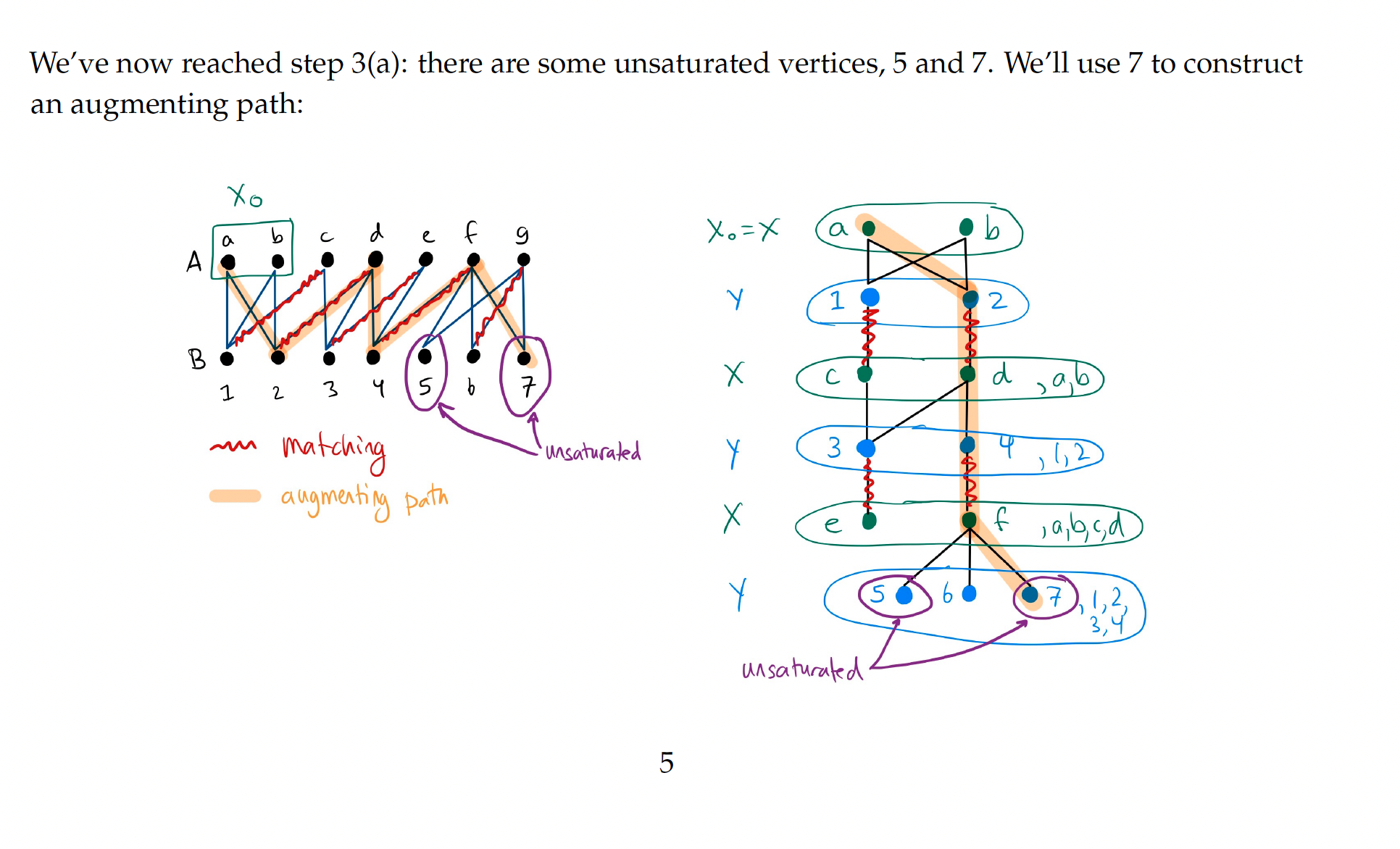
1. Let $X_0$ be the set of all unsaturated vertices in $A$.
2. Set $X\leftarrow X_0$ and $Y\leftarrow \varnothing$.
3. Find all neighbours of $X$ in $B$ not currently in $Y$.
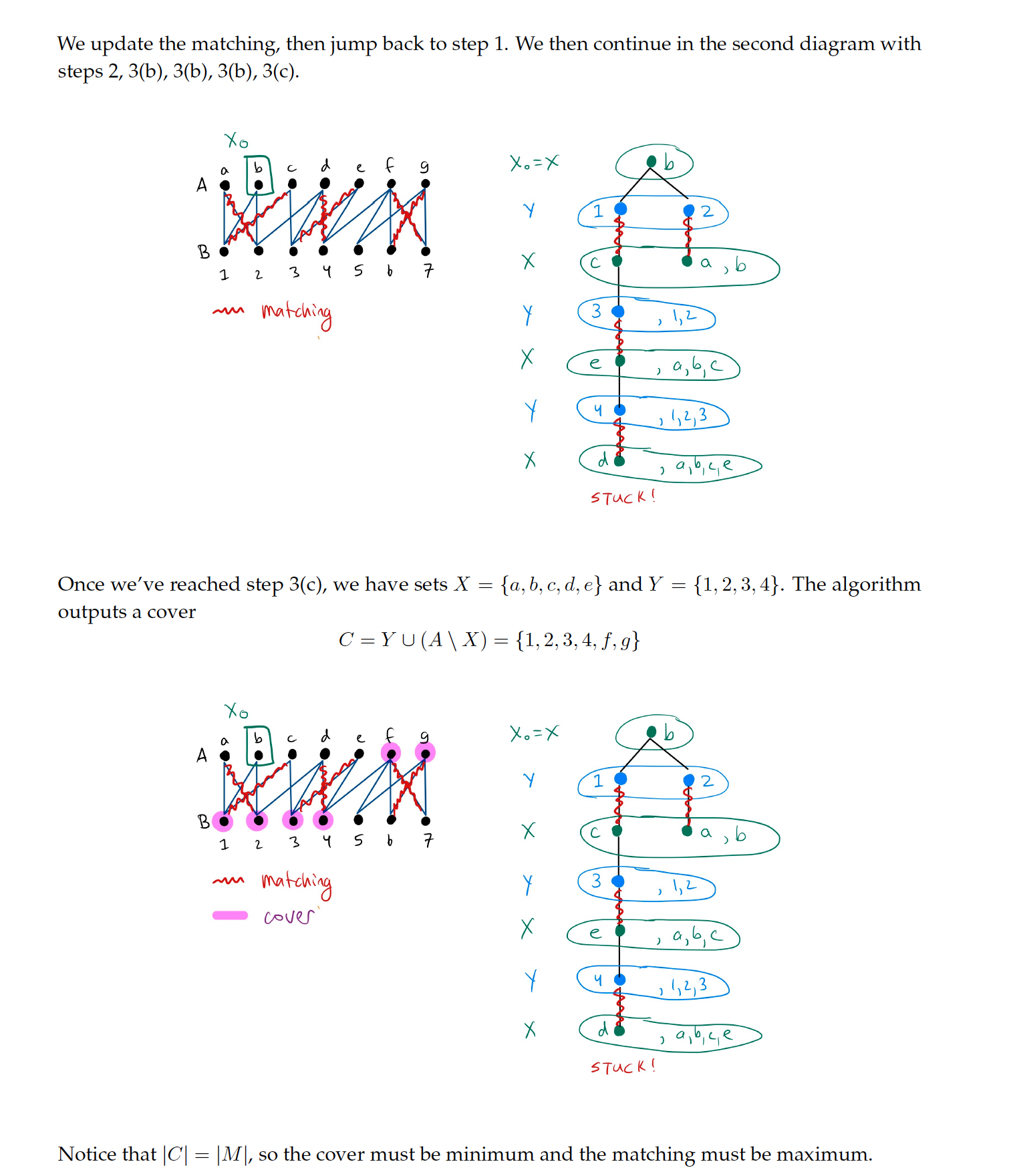
   • (a) If one such vertex is unsaturated, then we have found an augmenting path. Make a larger matching by swapping edges in the augmenting path. Then start over at step 1.
   • (b) If all such vertices are saturated, then put all of them in $Y$. Add their matching neighbours to $X$. Go to step 3.
   • (c) If no such vertices exist, then stop. The matching is maximum, and the minimum cover is $Y\cup (A\backslash X)$.

Example