Graph Matching

Definitions

Definition

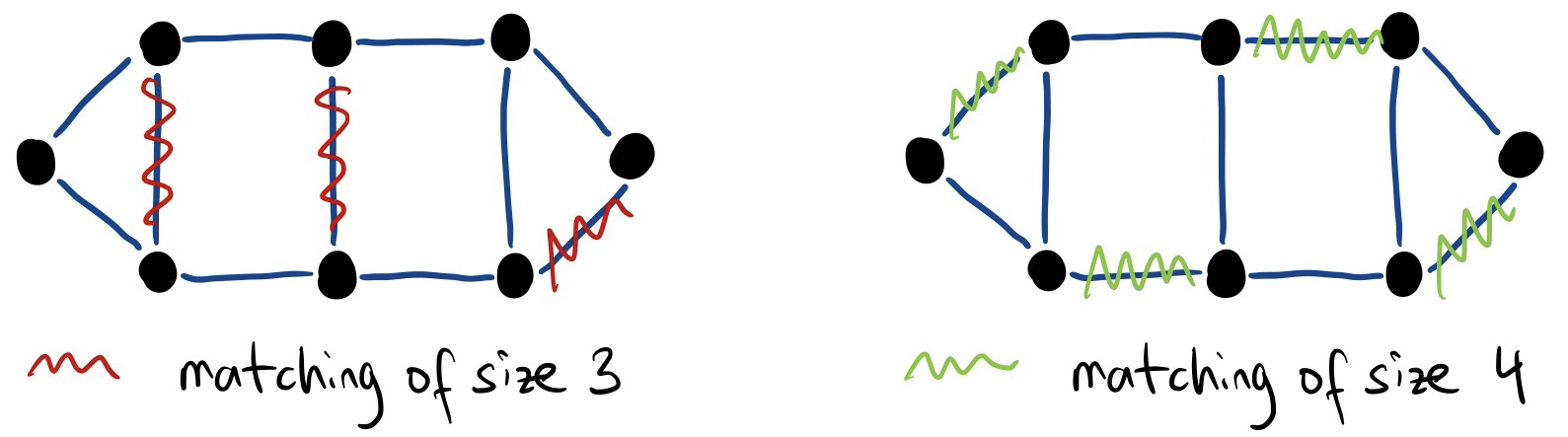
A matching of a graph is a set of edges in which no two edges share a common vertex.

Definition 2

In a matching $M$, a vertex $v$ is saturated by $M$ if $v$ is incident with an edge in $M$.

Definition 3

A matching is a perfect matching if it saturates every vertex.

If the graph does not have a perfect matching, how do we know we’ve got a maximum matching?

• We’ll look at a dual property with Graph Covers

Familiarize yourself with Graph Covers first.

Neighbour Set

Let $D\subseteq V(G)$. The neighbour set $N(D)$ of $D$ is the set of all vertices adjacent to at least one vertex of $D$: $N(D)=\{v:uv\in E(G)\wedge u\in D\}$

Theorems and Lemmas

Lemma 8.2.1

If $M$ is a matching of $G$ and $C$ is a cover of $G$, then $|M|\le |C|$.

Lemma 8.2.2

If $M$ is a matching and $C$ is a cover and $|M|=|C|$, then $M$ is a maximum matching and $C$ is a minimum cover.

Lemma 8.1.1

If a matching $M$ has an Augmenting Path, then $M$ is not maximum.

• An alternating path $P$ with respect to a matching $M$ is a match where consecutively alternate between being in $M$ and not in $M$
• An augmenting path is an alternating path that starts and ends with distinct unsaturated vertices

Given a matching $M$ and an augmenting path $P$, the new matching is $M^{\prime }=(M\cup (E(P)\backslash M))\backslash (E(P)\cap M)$

Konig's Theorem (Lemma 8.1.1)

In a bipartite graph, the size of a maximum matching is equal to the size of a minimum cover.

• Proven using the Bipartite Matching Algorithm

Corollary 1

Let $G$ be a Bipartite Graph on $m$ edges with bipartition $(A,B)$ such that $|A|=|B|=n$. Then $G$ has a matching of size at least $m/n$.

Hall's Theorem, Theorem 8.4.1

A bipartite graph $G$ with bipartition $(A,B)$ has a matching saturating every vertex in $A$ if and only if every subset $D\subseteq A$ satisfies $|N(D)|\ge |D|$. (This is called “Hall’s condition”.)

Corollary 8.6.1

A Bipartite Graph $G$ with bipartition $(A,B)$ has a perfect matching if and only if $|A|=|B|$ and every subset $D\subseteq A$ satisfies $|N(D)|\ge |D|$.

Theorem 8.6.2

If $G$ is a $k$-regular bipartite graph with $k\ge 1$, then $G$ has a perfect matching.

Related

• Bipartite Matching Algorithm
• 3D Matching