Boolean Algebra
In 1849, George Boole published a scheme for the algebraic description of processes involved in logical thought and reasoning, known as Boolean algebra.
Boolean Algebra poses a set of rules used to simplify the given logic expression without changing its functionality.

Axioms of Boolean Algebra
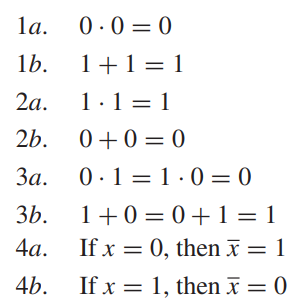
Single-Variable Theorems
If is a variable in , then the following theorems hold:
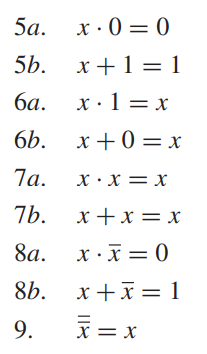
Principle of Duality
Given a logic expression, its dual is obtained by replacing all + operators with · operators, and vice versa, and by replacing all 0s with 1s, and vice versa.
The dual of any true statement (axiom or theorem) in Boolean algebra is also a true statement. This is based on De Morgan’s Laws (DML).
Why duality?
Duality implies that at least two different ways exist to express every logic function with Boolean algebra. Often, one expression leads to a simpler physical implementation than the other and is thus preferable.
Two- and Three-Variable Properties
If x, y, and z are the variables in , then the following properties hold:
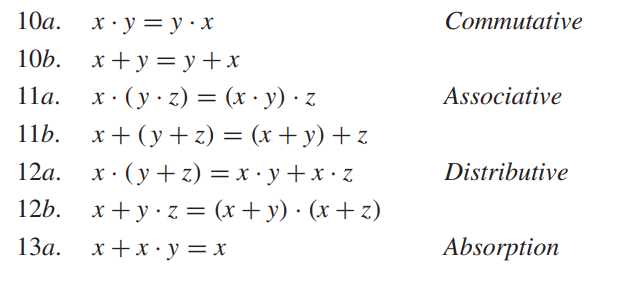
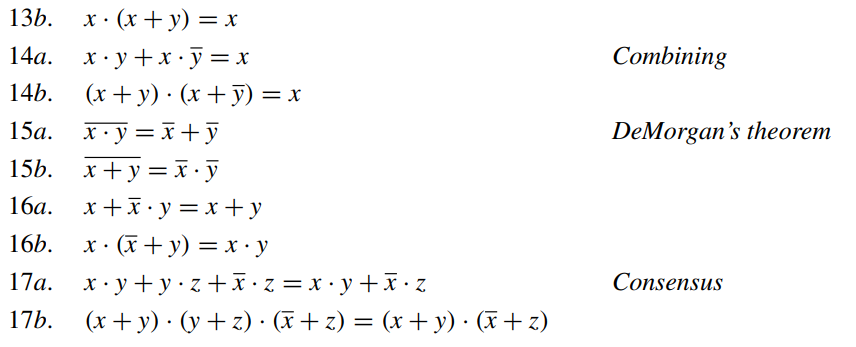
This review on boolean algebra is super helpful.