Karnaugh Map
Provides systemic way to optimize a logic function.
Implemented as SOP Form.
Boolean Algebra results are not always minimum.
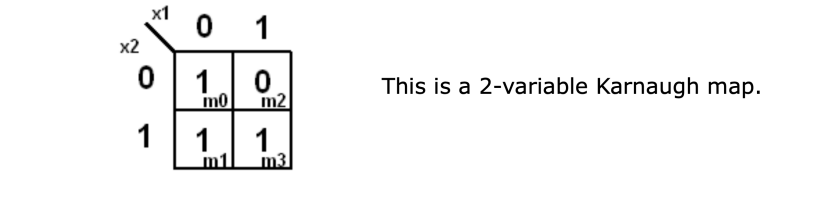
Cell Adjacency: The cells in a Karnaugh map are arranged so that there is only a singlevariable change between adjacent cells. So 00 → 01 → 11 → 10 is good, 01 → 10 is bad because 2 variables change at the same time.
Pairing Pairing can only be done vertically or horizontally. 2 1s → 4 1s → 8 1s → 16 1s
Prime Implicants
The group of 1s is called implicants. Prime Implicants: Largest possible groups of 1 Essential Prime Implicant: At least single 1 which cannot be combined in any way
Steps
- Find out number of variables
- Find out number of cells in K’ Map
- Draw the table and solve
Karnaugh Map Simplification of SOP Expressions
Grouping the 1s, you can group 1s on the Karnaugh map according to the following rules by enclosing those adjacent cells containing 1s. The goal is to maximize the size of the groups and to minimize the number of groups.
- A group must contain either 1, 2, 4, 8, or 16 cells, which are all powers of two. In the case of a 3-variable map, 23 = 8 cells is the maximum group.
- Each cell in a group must be adjacent to one or more cells in that same group.
- Always include the largest possible number of 1s in a group in accordance with rule 1.
- Each 1 on the map must be included in at least one group. The 1s already in a group can be included in another group as long as the overlapping groups include noncommon 1s
Determine the minimum product term for each group. a. For a 3-variable map: (1) A l-cell group yields a 3-variable product term (2) A 2-cell group yields a 2-variable product term (3) A 4-cell group yields a 1-variable term (4) An 8-cell group yields a value of 1 for the expression
Don’t Cares
Sometimes a situation arises in which some input variable combinations are not allowed. The “don’t care” terms can be used to advantage on the Karnaugh map. When grouping the 1 s, the Xs can be treated as 1s to make a larger grouping or as 0s if they cannot be used to advantage. The larger a group, the simpler the resulting term will be.
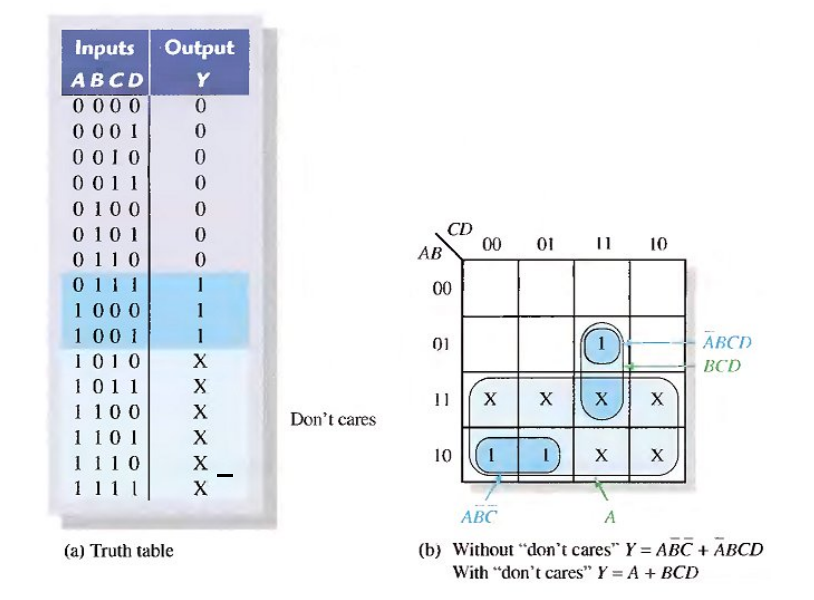
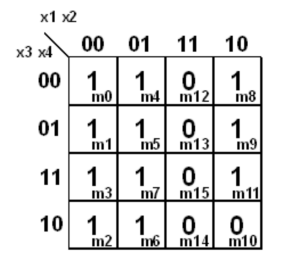
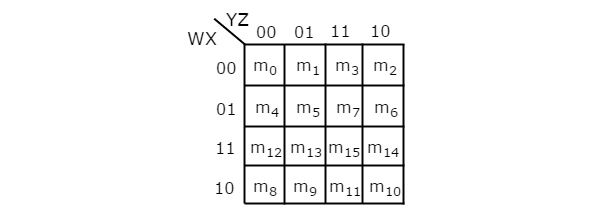
4-Variable K Map
Similar to 3-variable one.
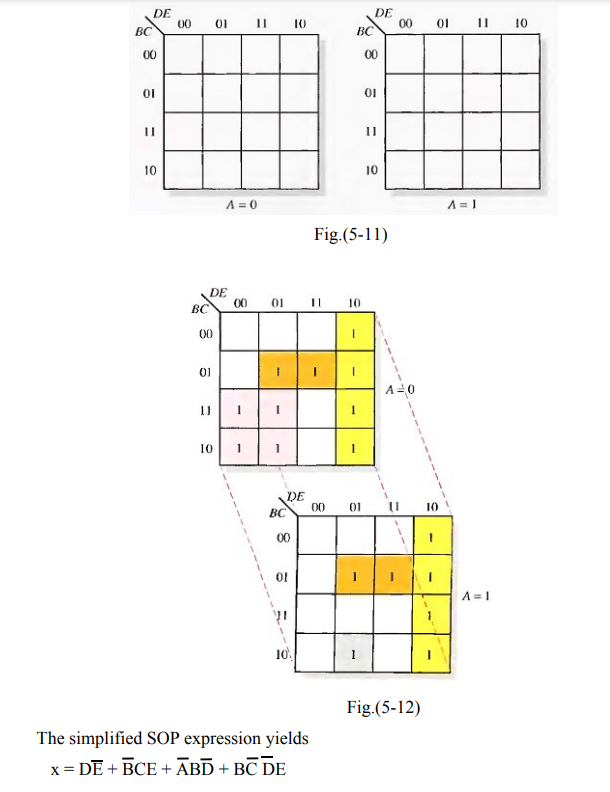
5-Variable KMap
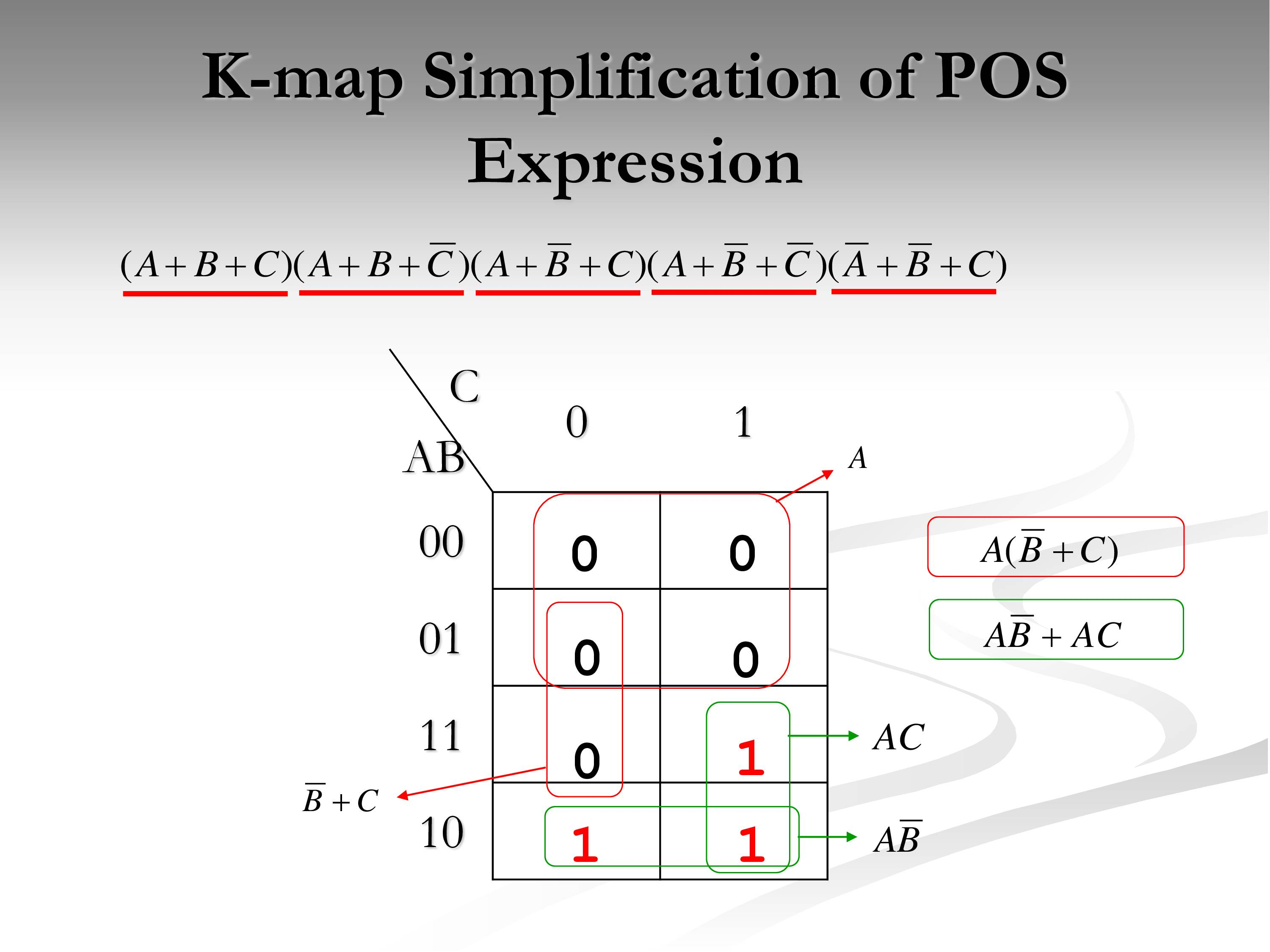
POS K’Map
This is another form of the KMap, but we use 0s instead of 1s. Check the image, and instead when we write the equation, we set the non-varying thing to 0, and use + fore each letter, and multiply the various terms together.
Look at the red box for the thing to make sense to you.
