The Chain Rule

$[f(g(x)){]}^{\prime }=f^{\prime }(g(x))\cdot g^{\prime }(x)$

In other words, $\frac{dy}{dx}=\frac{dy}{du}\frac{du}{dx}$

This is the basis for Backpropagation.

Intuitively, the chain rule states that knowing the instantaneous rate of change of z relative to y and that of y relative to x allows one to calculate the instantaneous rate of change of z relative to x as the product of the two rates of change.

As put by George F. Simmons: “if a car travels twice as fast as a bicycle and the bicycle is four times as fast as a walking man, then the car travels 2 × 4 = 8 times as fast as the man.”

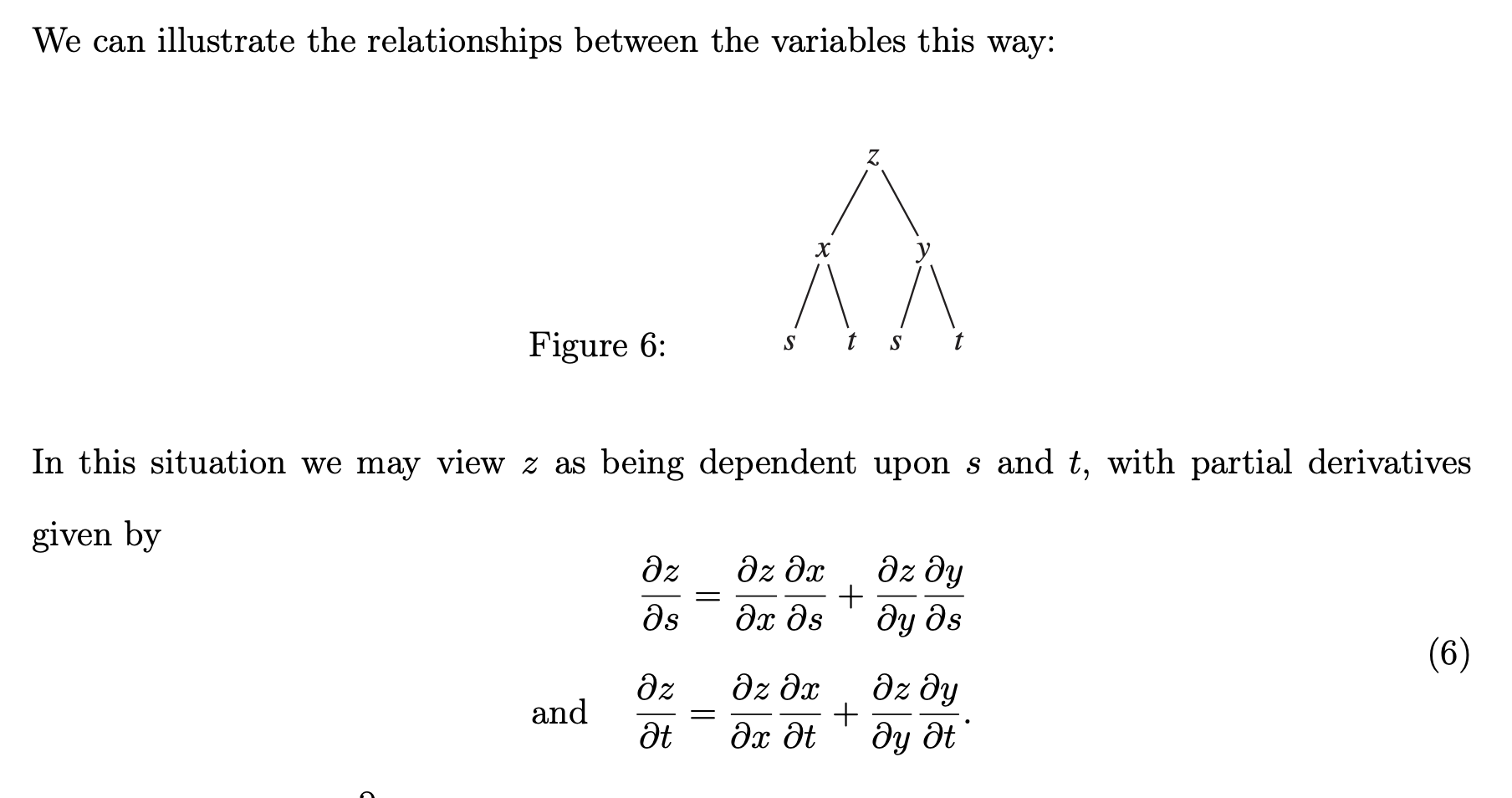
Multivariate Chain Rule

Chain Rule for Paths

The most basic form of the Chain Rule for multivariate calculus is written as $\frac{dz}{dt}=\frac{dz}{dx}\frac{dx}{dt}+\frac{dz}{dy}\frac{dy}{dt}$

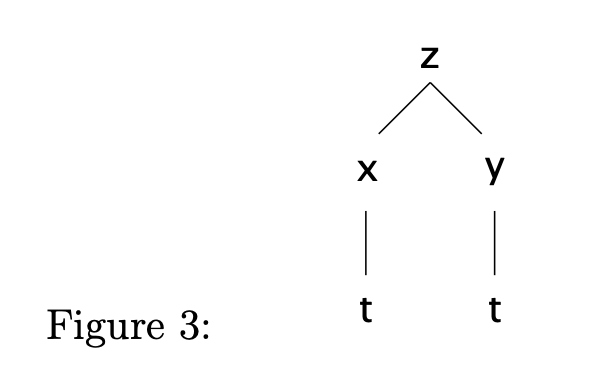When we have multiple variables, we simply draw chains with the relevant variables.