Conditional Probability

Conditional probability is the degree of belief in a proposition given some evidence that has already been revealed.

Conditional Probability

$P(A\mid B)$ is the probability of $A$ given $B$ (i.e. given that $B$ is true).

$P(A\mid B)=\frac{P(A\cap B)}{P(B)}$

Visualization: 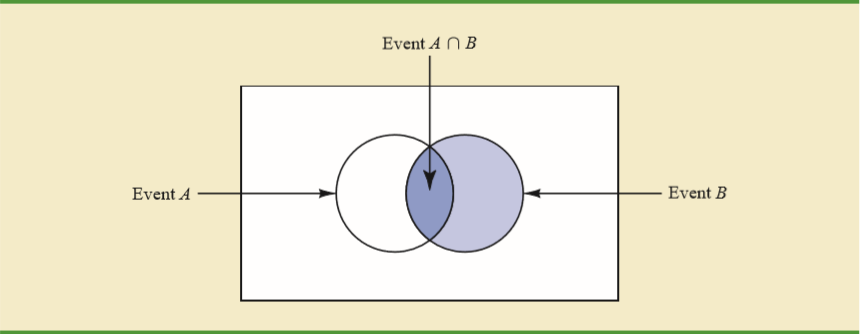Visualize as the dark blue area (intersection area) over the light blue area ($P(B)$).

Other way to arrange, multiplying events: $P(A\cap B)=P(B)P(A|B)=P(A)P(B|A)$

This is basically the Chain Rule for probability! Idea from here

Other useful equation: $P(A^C|B)=1-P(A|B)$

Related

• Bayes’ Theorem