Circuit Theorems

This introduces several advanced methods to solve circuits.

• Linear System

Linearity

You assume a value, and then in the end multiple but the proportions.

Linearity does not apply to the computation of power since it is a non linear function of current or voltage.

Principle of Superposition

The current or voltage in a linear circuit can be computed as the algebraic sum of the individual contributions of each independence source acting alone.

To deactivate independent sources:

• Voltage Source $v_s=0$ → Short Circuit
• Current Source $i_s=0$ → Open Circuit

Do not deactivate dependent sources. They are not considered as input to the circuit system.

Source Transformation

It can be shown that a combination of a voltage in series with a resistance is equivalent to a combination of a current source in parallel with a resistance, i.e. 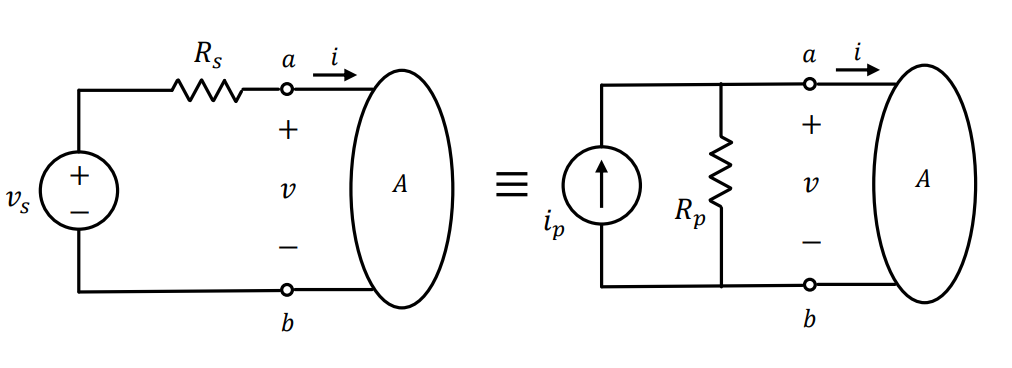Resistor remains the same value, but change $v$ and $i$ such that $i=\frac{v}{R}$

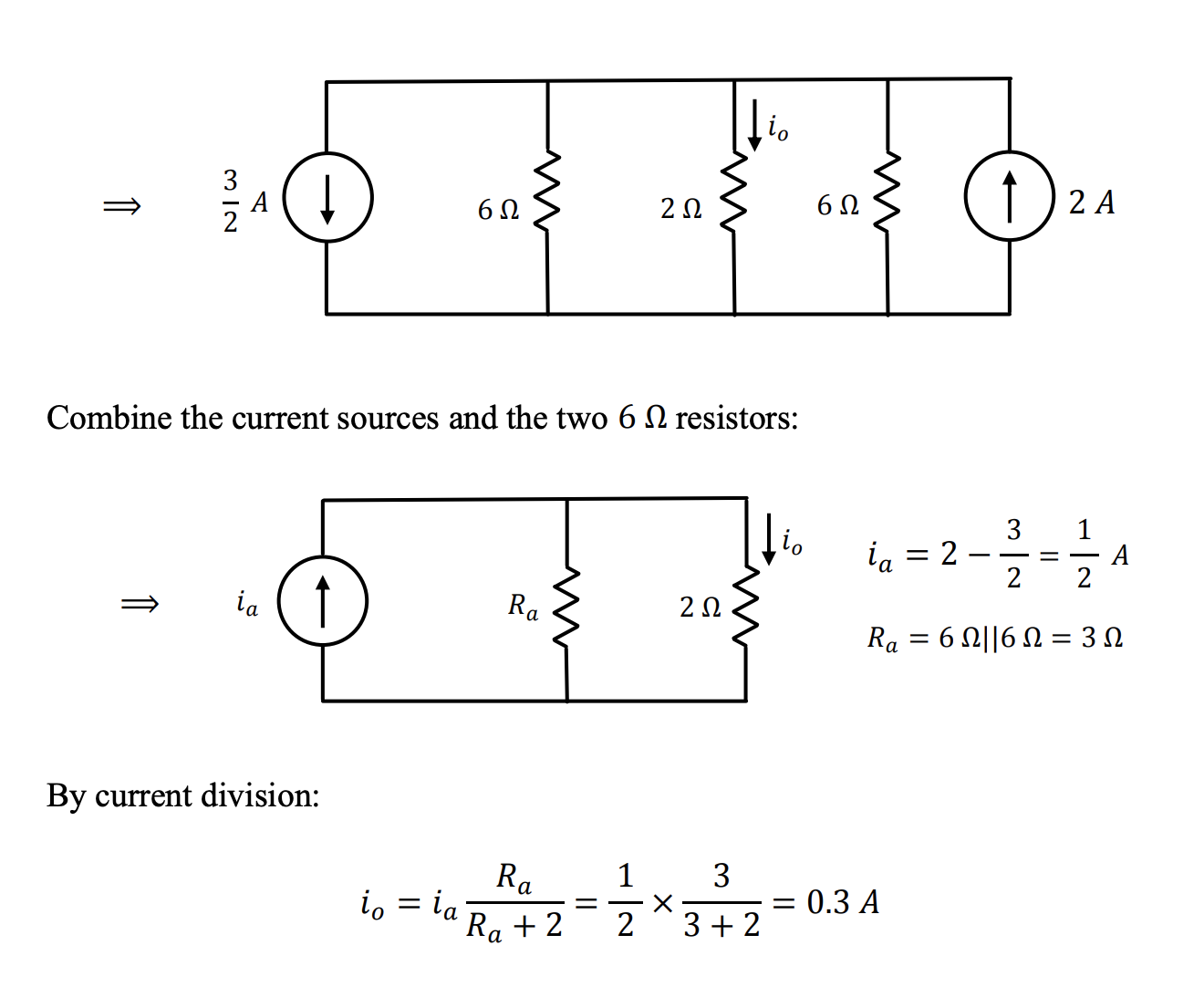
title: Some things to remember
When solving problems, sometimes you will need to use this fact:
- A resistor in parallel with a voltage source has no effect on the rest of the circuit (so you can remove it!!)
- A resistor in series with a current source has no effect on the rest of the circuit (so you can remove it!!)

title: Remarks
1.$v_s = R_pi_p$ and $R_s = R_p$
2. IMPORTANT Watch for the direction of the current source. The tip of the arrow of the current source must be pointing to the terminal at which the voltage source has positive polarity.
3. Source transformation can be applied to **independent sources**.

Other Theorems

• Thevenin’s Theorem
• Norton’s Theorem