Conditioning of Problems

Learned this in CS370.

Problems may be ill-conditioned or well-conditioned. For problem $P$, with input $I$ and output $O$, if a change to the input, $I$, gives a “small” change in the output $O$, $P$ is well-conditioned. Otherwise, $P$ is ill-conditioned.

This is a property of the problem itself, independent of any specific implementation (algorithm, hardware, etc.)

Conditioning is all relative.

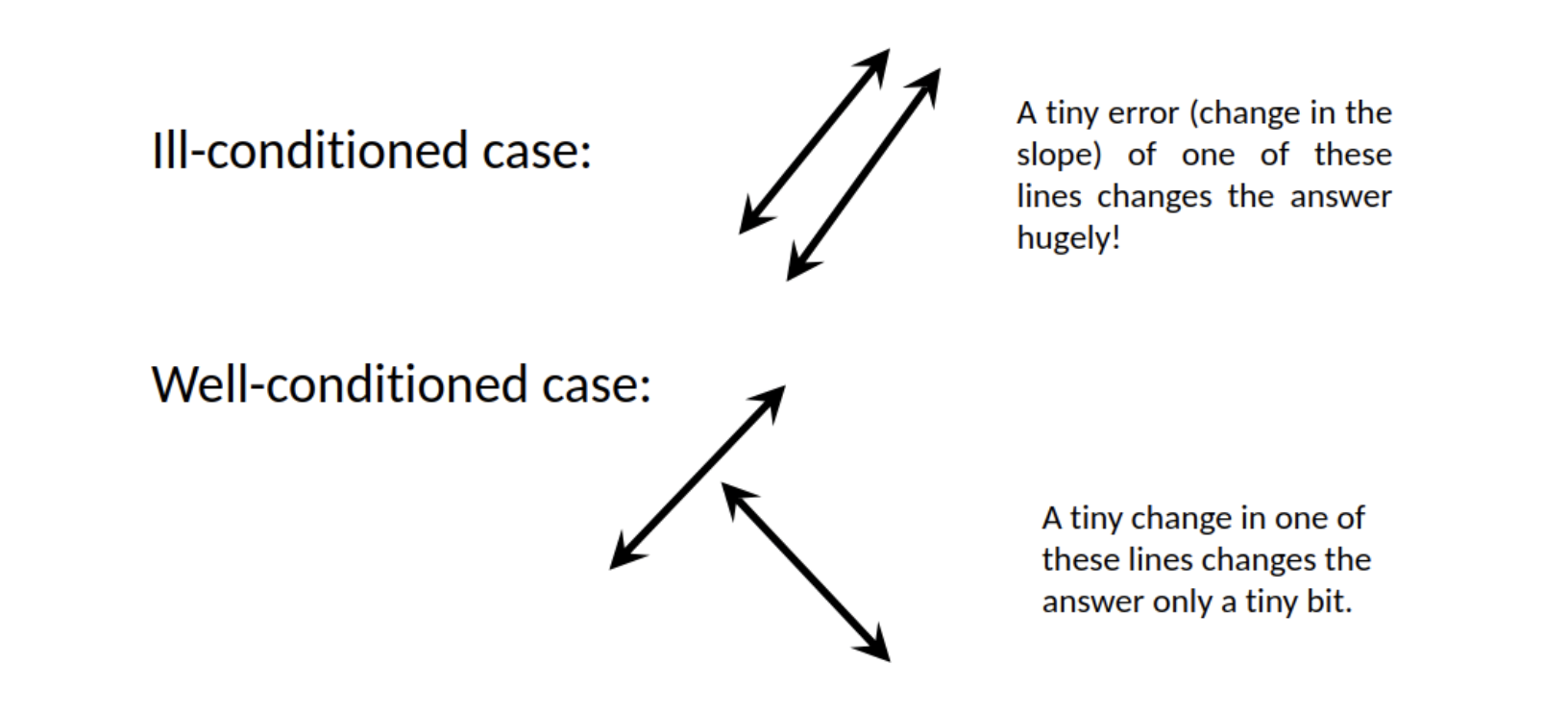
• In the ill-conditioned case, a very small change drastically affects the output

Conditioning of Problems vs. Stability of Algorithms

It is important to distinguish conditioning, which is a property of a problem itself, from the somewhat related concept of stability, which is instead a property of an algorithm or a numerical process used to (approximately) solve a problem.

Generally, a ill-conditioned problem will be solved by an unstable algorithm, but there are exceptions.