Configuration Space

https://uwaterloo.ca/electrical-computer-engineering/sites/ca.electrical-computer-engineering/files/uploads/files/ece_486_1215.pdf #todo ask instructor for solutions manual

A robot is mechanically constructed by connecting a set of bodies, called links, to each other using various types of joints.

We describe the position of these links and joints using the configuration space.

Definition 2.1. The configuration of a robot is a complete specification of the position of every point of the robot. The minimum number $n$ of real-valued coordinates needed to represent the configuration is the number of degrees of freedom (dof) of the robot. The $n$-dimensional space containing all possible configurations of the robot is called the configuration space (C-space). The configuration of a robot is represented by a point in its C-space.

title: Intuitively
Intuitively, the *configuration space* of a robot is the set of all configurations and/or positions that the robot can attain.
 
Ex: simple planar arm with two revolute joints, all the possible configurations of this robot can be represented with a tuple of joint angles $\theta_1$ and $\theta_2$.

Degrees of Freedom of Robot

Configuration Space Topology

The shape of the configuration space is also important. We call this study its topology. While both a plane and the surface of a sphere are two dimensional, clearly they do not have the same shape – the plane extends infinitely while the sphere wraps around.

The topology of a space is a fundamental property of the space itself and is independent of how we choose coordinates to represent points in the space.

Configuration Space Representation

To perform computations, we must have a numerical representation of the space, consisting of a set of real numbers.

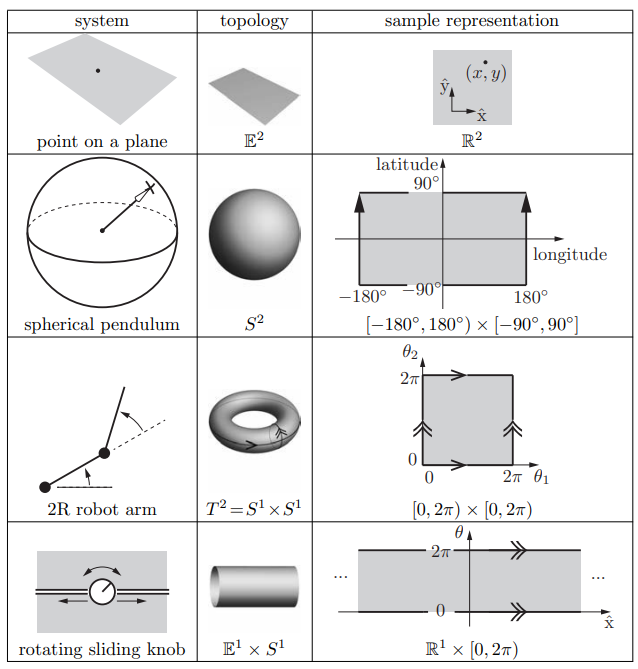
For Euclidean Space, denoted $\mathbb{E}$, this is straightforward, choose a vector to represent points.

However, what about the others? Like a sphere. We distinguish two ways to represent our configuration space.

Explicit Parametrization

Use $n$ coordinates, or parameters, to represent an $n$-dimensional space.

This, sometimes, can be hard to implement. There are also problems like running into singularities. Imagine a sphere. The north and south poles are singularities of the representation, since we use coordinates [-180, 180] for example.

The location of these singularities has nothing to do with the sphere itself, which looks the same everywhere, and everything to do with the chosen representation of it.

Why is this a problem? As the time rate of change of coordinates, since these representations may tend to infinity near singularities even if the point on the sphere is moving at a constant speed. To address this problem, we look at 2 solutions.

• Use more than one coordinate chart on the space. As the configuration representation approaches a singularity in one chart, e.g., the North or South Pole, you simply switch to another chart where the North and South Poles are far from singularities The other is Implicit representation.

Implicit representation

this is what is used in the book. Implicit representation views the $n$-dimensional space as embedded in a Euclidean space of more than $n$ dimensions.

Advantage:

• No singularities in the representation – a point moving smoothly around the sphere is represented by a smoothly changing $(x,y,z)$, even at the North and South poles

Disadvantage:

• The representation has more numbers than the number of degrees of freedom

Configuration and Velocity Constraints

As we said, it’s easier to implement an implicit representation.

Holonomic constraints: Pfaffian constraints: $A(\theta )\dot{\theta }=0$

holonomic constraints of the form $g(\theta )=0$ are also called integrable constraints

A Pfaffian constraint that is nonintegrable is called a nonholonomic constraint

Task Space and Workspace

The task space is a space in which the robot’s task can be naturally expressed. The decision of how to define the task space is driven by the task, independently of the robot.

Drawing with a pen on a piece of paper has a task space of $\mathbb{R}^2$.

The workspace is a specification of the configurations that the end-effector of the robot can reach. The definition of the workspace is primarily driven by the robot’s structure, independently of the task.

The task space and the workspace are distinct from the robot’s C-space. A point in the task space or the workspace may be achievable by more than one robot configuration, meaning that the point is not a full specification of the robot’s configuration. For example, for an open-chain robot with seven joints, the six-dof position and orientation of its end-effector does not fully specify the robot’s configuration.