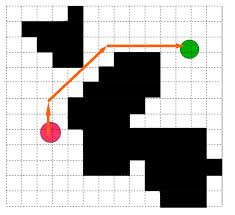
Motion / Path Planning
The Motion Planning problem is to find an optimal path for the robot to move through gradually from start to goal while avoiding any obstacles in between
- This seems pretty easy but it’s hard
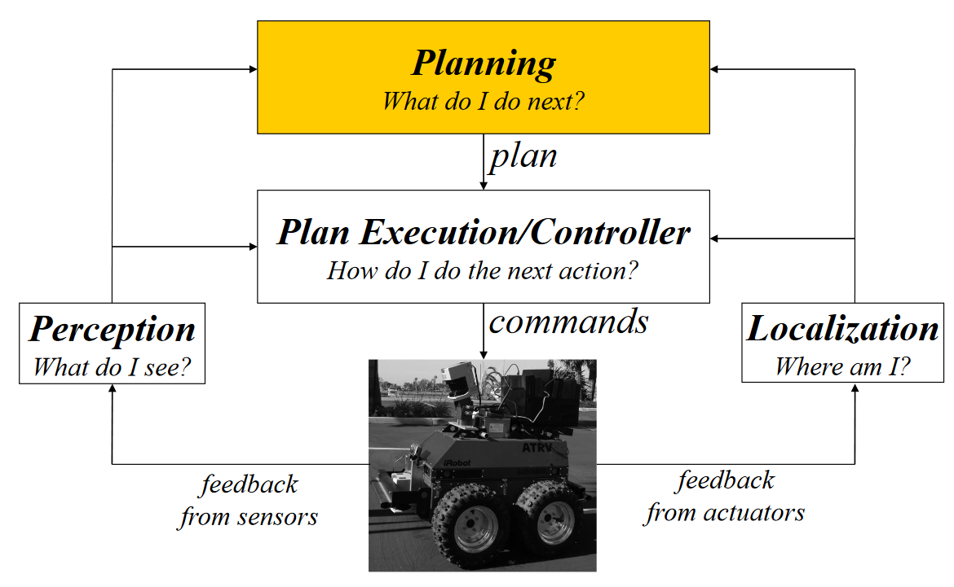There’s another image that I have in Autonomous Vehicles.
Path planning approaches are gauged by
- Completeness: Guaranteed to find a solution? (if one exists)
- Optimality: Finds the best solution (for example, shortest)
At a high level, we can divide path planning into 2 different categories: sampling-based and search-based path planning.
Thinking about path planning
The naive way is to think about path planning in terms of simple 2D grids.
But this is not always the case in the real world, where the domain is continuous, and your robot might have multiple actuators, and is non-holonomic.
Search-Based Path Planning
In search-Based planning, we divide the problem into 2 phases:
- Graph construction (trivial if you are already given a grid)
- Graph search
There are multiple ways you can construct a graph, including:
- Cellular Decomposition (most popular, where you discretize from continuous to discrete space to get a grid)
- Visibility Graph
- Voronoi Diagram
Once you have a graph constructed, you can use any of these search algorithms to do
Sampling-Based Path Planning
Sampling-Based algorithms are suitable for high-dimensional problems because the size of the graph they construct is not explicitly exponential in the number of dimensions. The con is that they are not very repeatable or provable.
Sampling based methods can be divided into two categories:
- Multi-query: multiple start and goal configurations can be connected without reconstructing the graph structure
- Single-query: the tree is built from scratch for every set of start and goal configurations
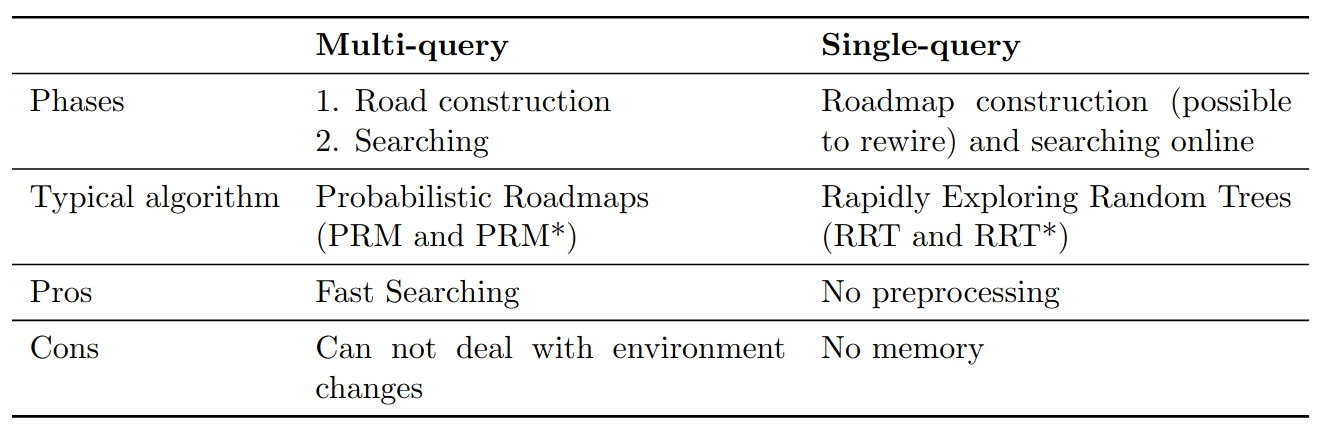
- Probabilistic Road Maps (PRM) for multi-query
- Rapidly Exploring Random Trees (RRT) for single-query
Self-Driving Cars
Many approaches in the field of path planning are based on splines.