Feature Point

Descriptor

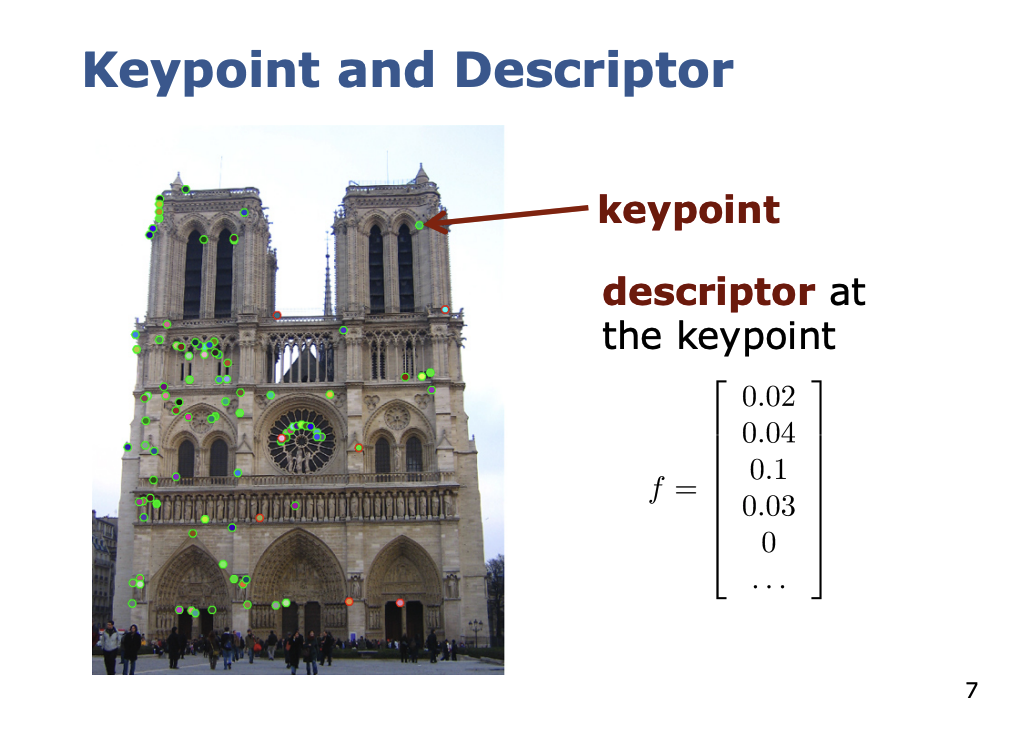
There are LOTS of popular feature descriptors

• HOG: Histogram of Oriented Gradients
• SIFT: Scale Invariant Feature Transform
• SURF: Speeded-Up Robust Features
• GLOH: Gradient Location and Orientation Histogram
• BRIEF: Binary Robust Independent Elementary Features
• ORB: Oriented FAST and rotated BRIEF
• BRISK: Binary Robust Invariant Scalable Keypoints
• FREAK: Fast REtinA Keypoint

Nowadays

There are also learning-based methods, which learn the features instead of hand-engineering them nowadays.

SIFT: Scale Invariant Feature Transform

• Hand-engineered

Image content is transformed into features that are invariant to

• image translation
• rotation
• scale

Partially invariant to

• illumination changes
• affine transformations and 3D projections

Suitable for detecting visual landmarks

• from different angles and distances
• with a different illumination

So how does it achieve that?

We are about to find out.

• $p,s,r$ and view-point dependent
• The 128-dim descriptor $f$ is mainly independent

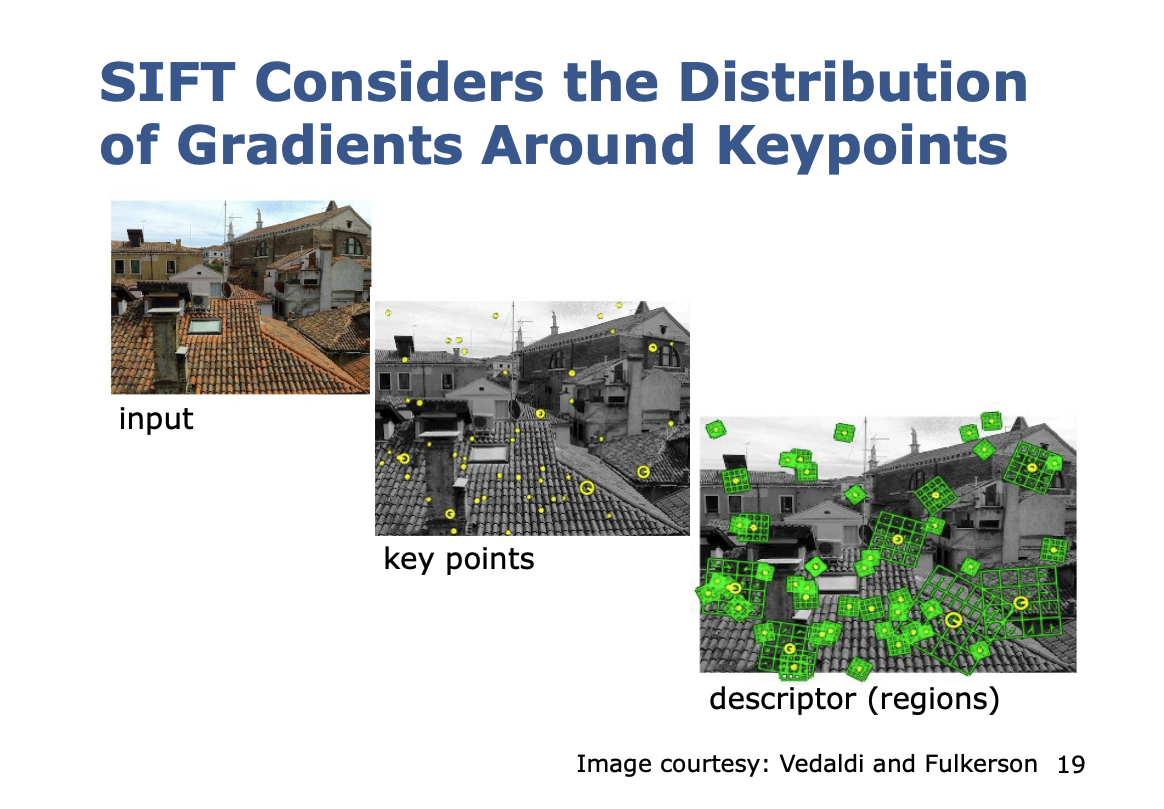
So how does it work? The Cyrill illustration are super helpful.

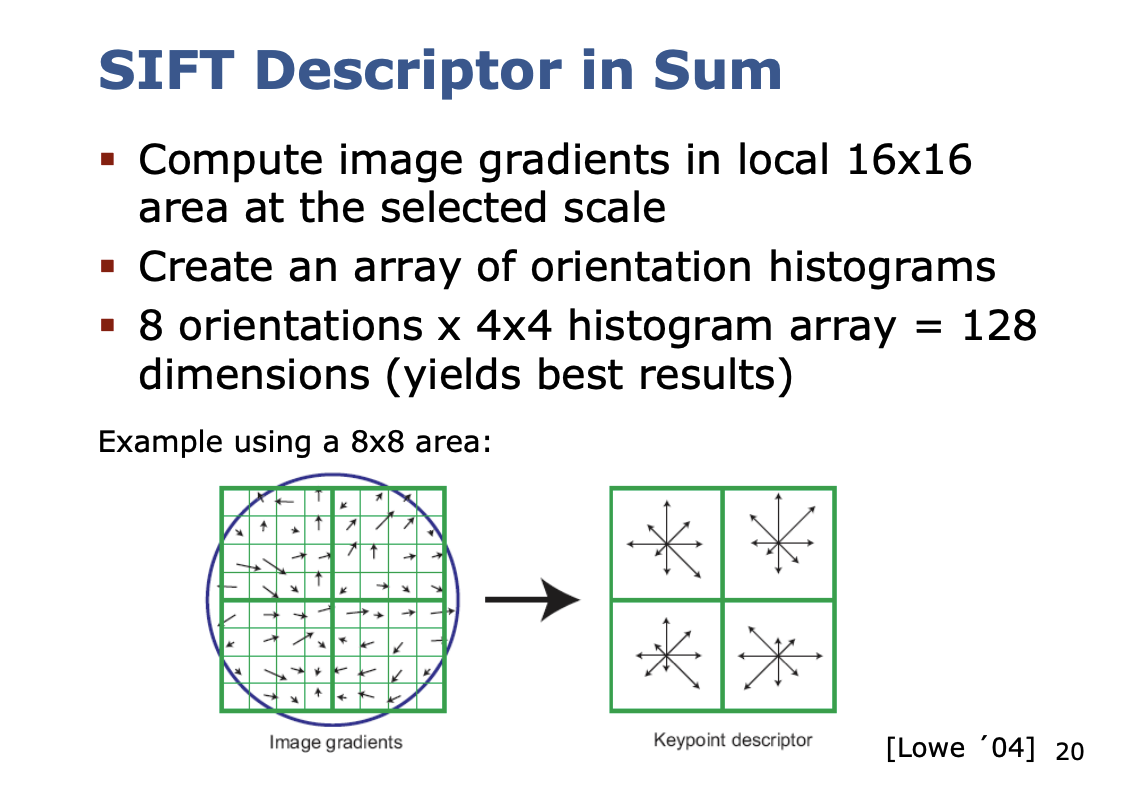
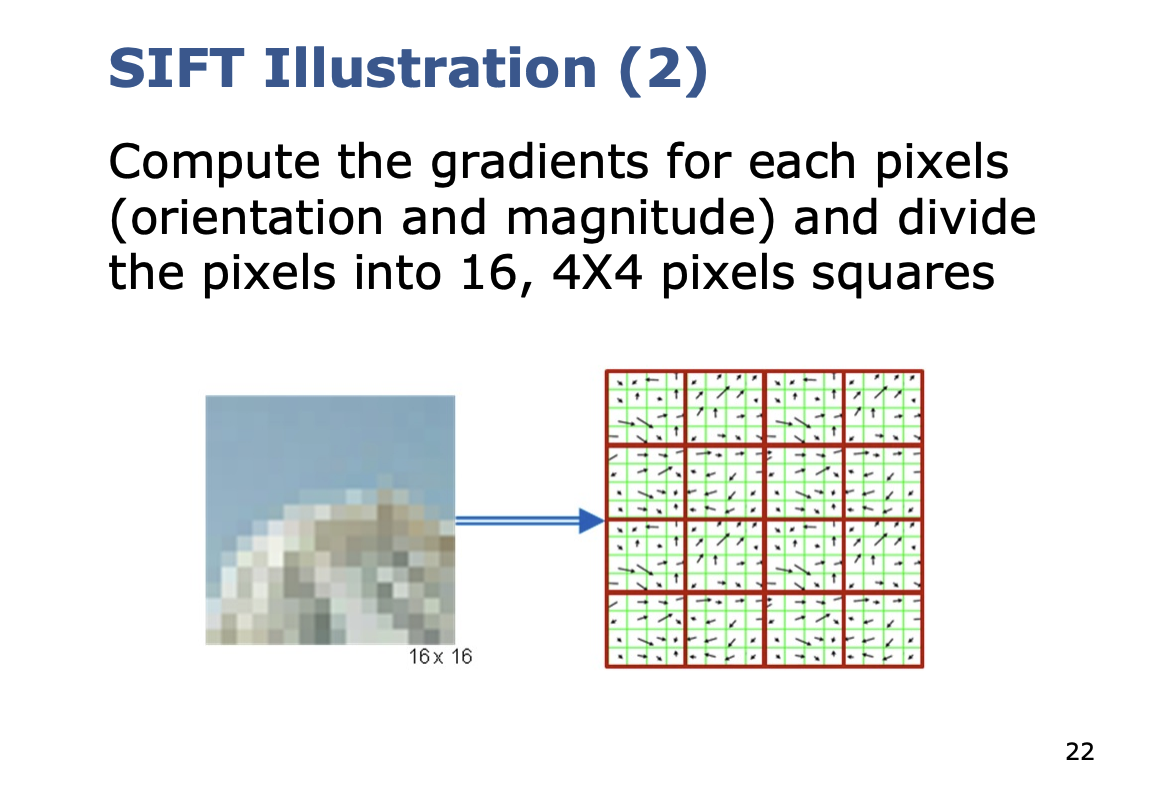
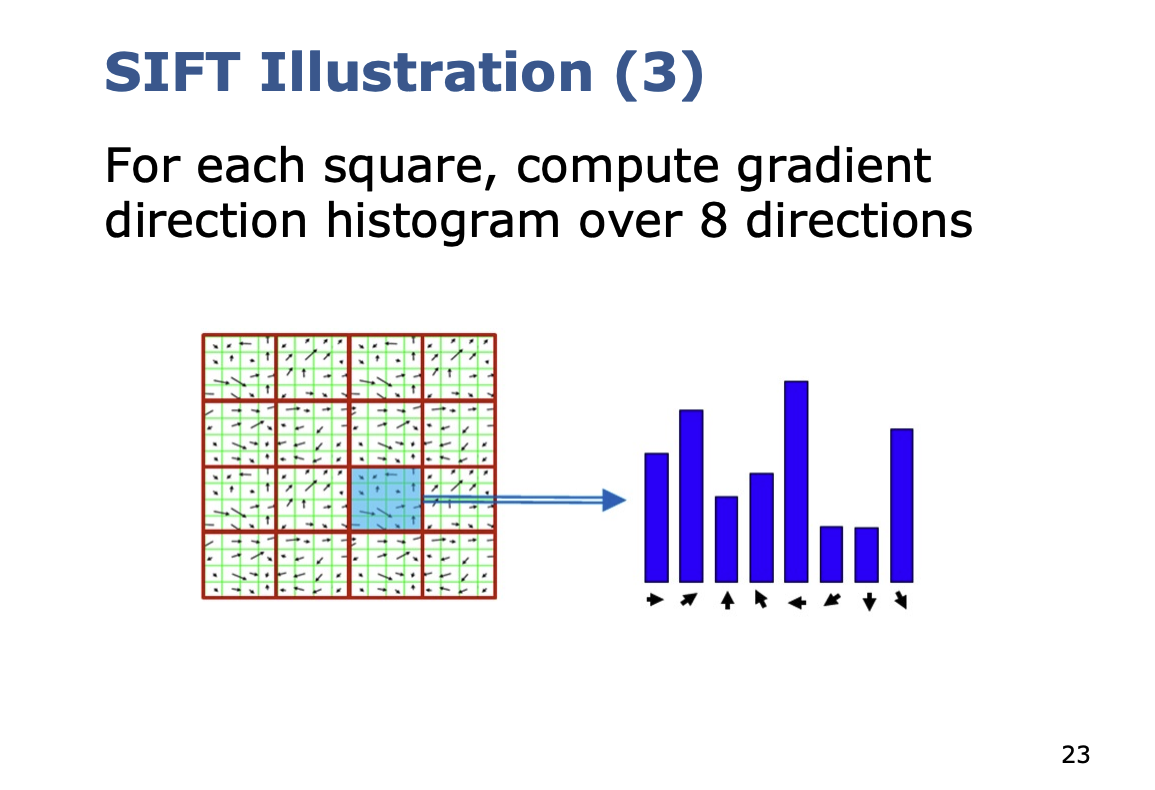
So high level:

So basically, you are computing histograms of gradients, and basically flatten the histograms.

But you can sometimes have wrong data associations, such as in the example below

You can do a ratio test to eliminate some of the wrong measures.

3 Step test to eliminate ambiguous matches for a query feature

1. Step: Find closest two descriptors to $q$, called p1 and p2 based on the Euclidian distance $d$
2. Step: Test if distance to best match is smaller than a threshold: $d(q,p_1)<T$
3. Step: Accept match only if the best match is substantially better than second: $\frac{d(q,p_1)}{d(q,p_2)}<\frac{1}{2}$

• Lowe’s Ratio test works well
• There will still remain few outliers
• Outliers require extra treatment

Binary Descriptors

This is about computing descriptors fast.

The issue is that SIFT takes a pretty long time. SIFT are not the way to go.

• GPU implementations of SIFT exist, but it is compute heavy

Fairly simple strategy

• Select a patch around a keypoint
• Select a set of pixel pairs in that patch
• For each pair, compare the intensities

$b=\{\begin{array}{ll}1& \text{if }I(s_1)<I(s_2)\\ 0& \text{otherwise}\end{array}$

• $I(s_1)$ refers to the intensity of pixel $s_1$

Concatenate all $b$’s to a bit string.

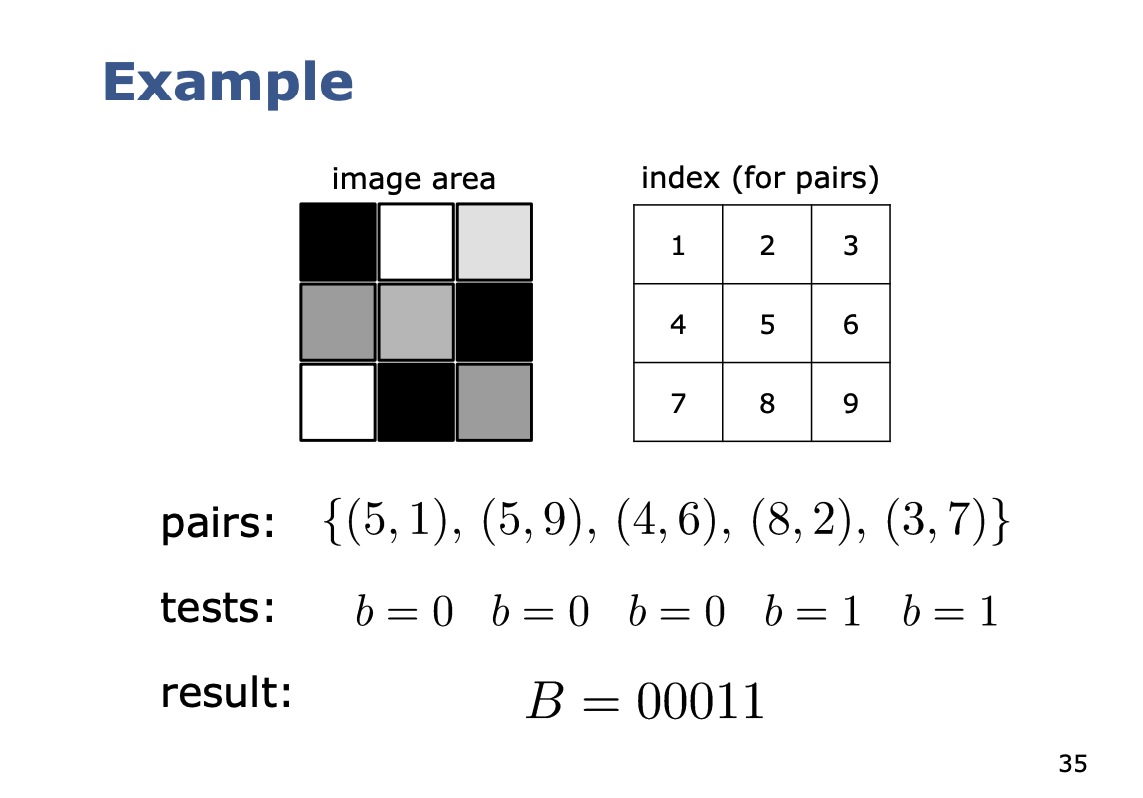
There is a simple strategy for how the pairs are chosen.

Key Advantages of Binary Descriptors

• Compact descriptor: The number of pairs gives the length in bits
• Fast to compute: Simply intensity value comparisons
• Trivial and fast to compare: Hamming Distance given by $d_{\text{hamming}}(B_1,B_2)=sum(xor(B_1,B_2))$

The key thing is, how do we select which pair of strings should we choose?

Different Binary Descriptors Differ Mainly by the Strategy of Selecting the Pairs.

BRIEF : Binary robust independent elementary features

• First binary image descriptor

• Proposed in 2010

• 256 bit descriptor

• So there are 256 different pairs

• Provides five different geometries as sampling strategies

• Noise: operations performed on a smoothed image to deal with noise

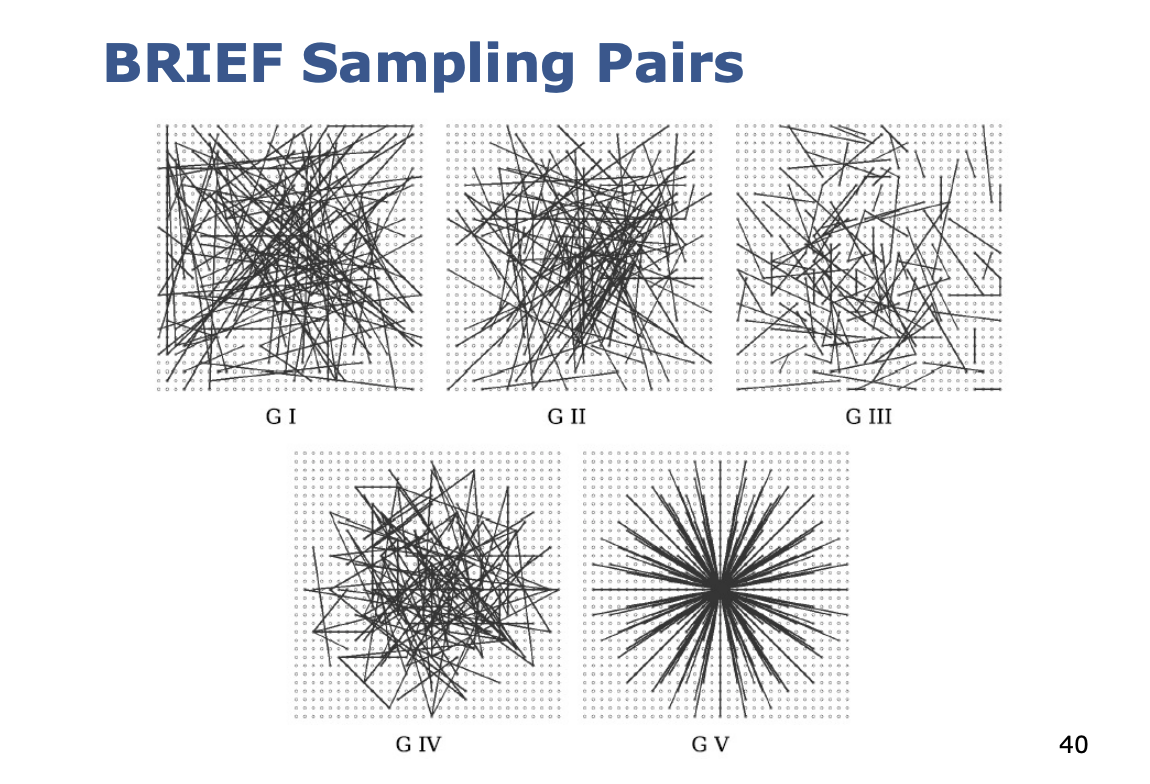
BRIEF Sampling Pairs

• G I: Uniform random sampling
• G II: Gaussian sampling
• G III: $s_1$ Gaussian; $s_2$ Gaussian centered around $s_1$
• G IV: Discrete location from a coarse polar gird
• G V: $s_1=(0,0)$ ; $s_2$ are all location from a coarse polar grid

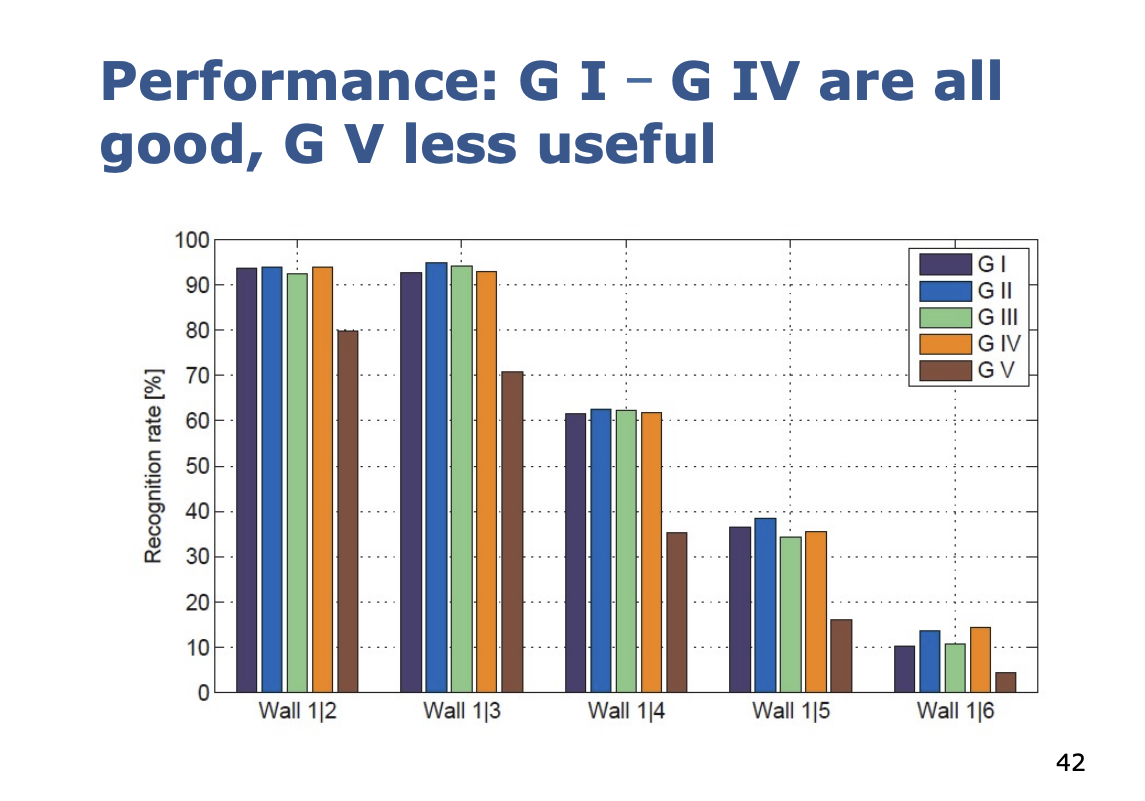
Now, the issue is that orientation is a problem. So we introduce ORB.

ORB: Oriented FAST Rotated BRIEF An extension to BRIEF that

• Adds rotation compensation
• Learns the optimal sampling pairs

I skipped the notes here…

ORB vs. SIFT

• ORB is 100x faster than SIFT
• ORB: 256 bit vs. SIFT: 4096 bit
• ORB is not scale invariant (achievable via an image pyramid)
• ORB mainly in-plane rotation invariant
• ORB has a similar matching performance as SIFT (w/o scale)
• Several modern online systems (e.g. SLAM) use binary features