Cache

Direct Mapped Cache

See video: https://www.youtube.com/watch?v=RqKeEIbcnS8&ab_channel=MatthewWatkins

For direct mapped, we map each memory location to exactly one location in the cache.

• So when we try to look up the word at a particular address, we know where to look in the cache using the mapping from address to cache location There are more addresses than number of entries in the cache, so in practice, we take the modulo, where $\text{Cache address mapped}=\text{(Block address)}\mathrm{mod}(\#\text{ blocks in cache})$

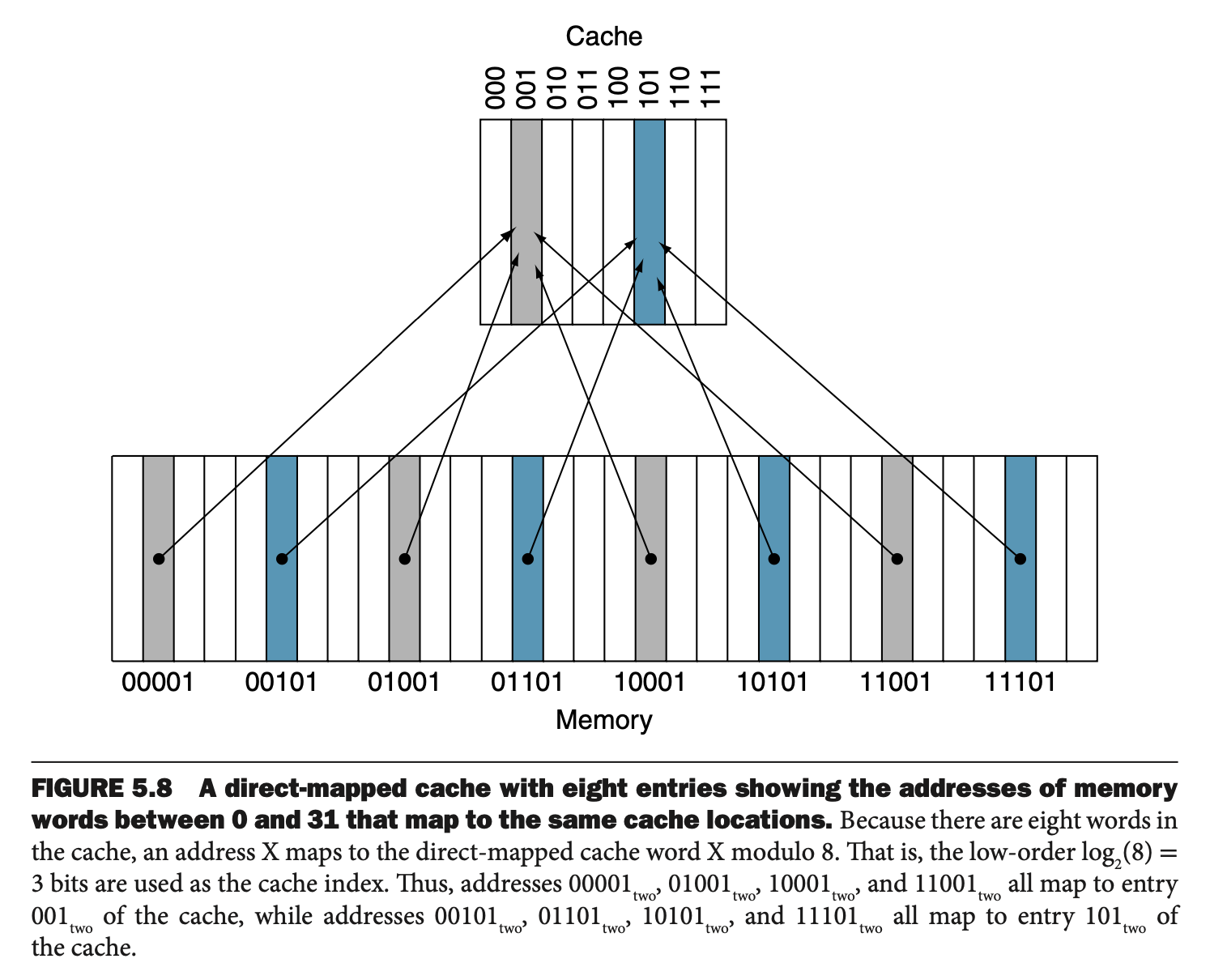
Since multiple memory locations map to a single cache entry (as you can see above), so how do we know which memory address the entry in the cache corresponds?

• We use a set of tags to the cache
• We also add a valid bit to indicate if the entry contains a valid address

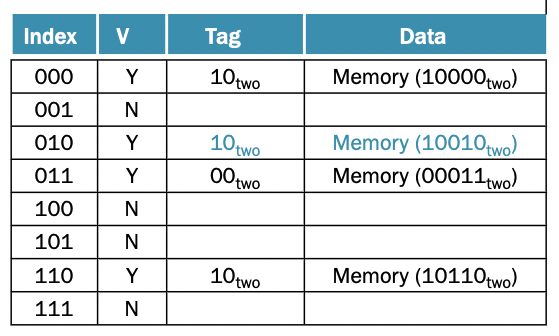
A referenced address is divided into

• A tag field, which is used to compare with the value of the tag field of the cache
• A cache index, which is used to select the block

So it is split like this!! Tag is whatever remains of at the beginning of the block.

In the example below, you have the tag 10, and the index 000, which represents memory address 10000.

However, in an actual 32-bit architecture, because words are aligned to multiples of four bytes, so 2 bits are used as Byte Offset

• In 64-bit architecture, where there are 8 bytes per word, we use 3 bits for the byte offset, this is used to index into the right byte

we actually only need to worry about 30bits for the address. Also, each block can have multiple words, so you also need to be able to index each block. In the end, you get that the number of bits in the tag field is given by $30-n-m$

• where $n$ is the number of bits used to index the cache, so a cache has $2^n$ blocks
• $m$ is the number of bits needed to represent the index of the words for each block, so each block has $2^m$ words
  • So if its just one-word blocks, then $m=0$

The total number of bits in a direct-mapped cache is $2^n\times (\text{block size + tag size + valid field size})$

• where block size is how much data you can actually store in a block
  • If a block can store 4 words, then the block size is 4 * 32 bits
• Tag size is given by the formula above
• Valid field size = 1 always (1 or 0 bit to indicate if this field is valid)

Typically, we don’t count the size of the tag and valid field.

What happens

What happens when there are multiple words per block??? You also need to do word indexing????? How do you check if there is a hit for that block?

So if there is a 1-word block, then you don’t need word indexing. Else, you want to assign the right number of bits to for the word. Ex: 4-word block means assigning 2 bits to for word-indexing.

OFFSET = word-index = word offset RIGHT?

So you have the index, followed by the offset.

• In 1-word block, there is no need for the offset column

And when checking for cache hit/miss, you ignore the offset, and just check the tag and the index, NOT the offset.

You still still have a cache hit even when two addresses are different.

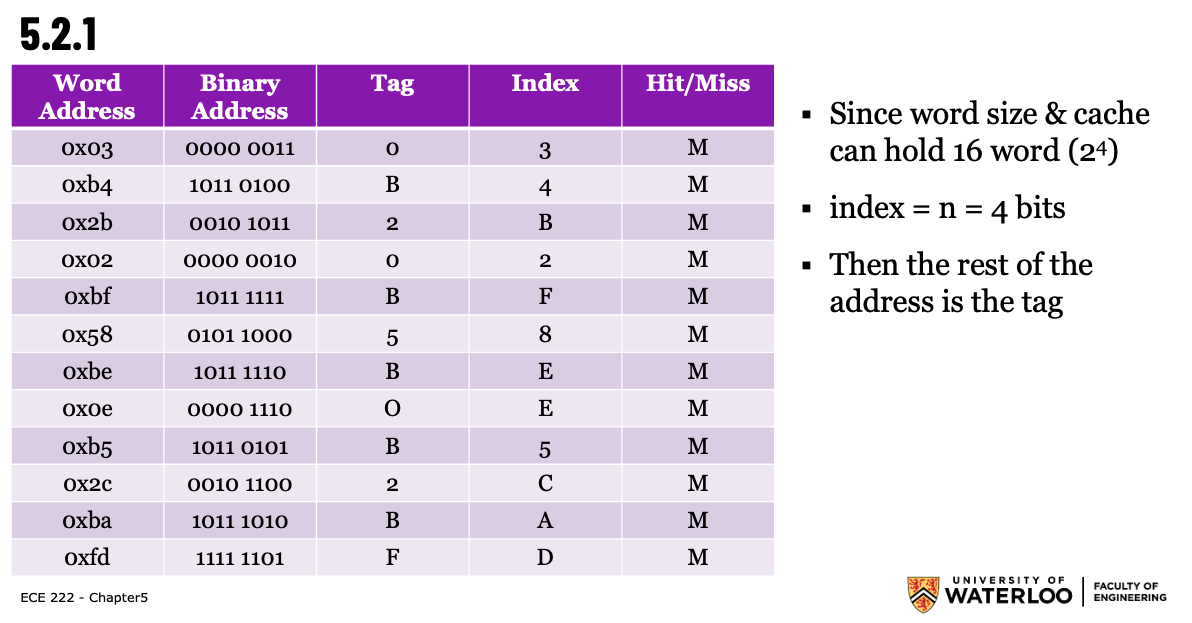
Example (Given as Word Addresses)

1-word blocks with a total size of 16 blocks:

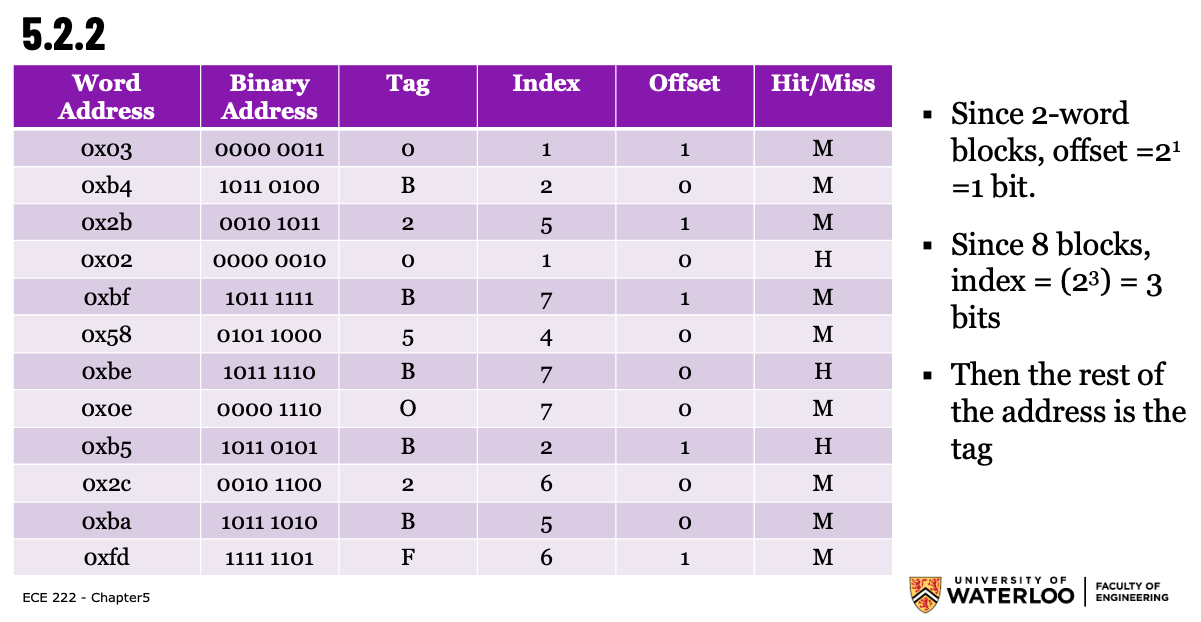
2-word blocks with a total size of 8 blocks:

• Notice that you index first, and then have the offset as the last bit

Byte-Addressed vs Word-Addressed

IMPORTANT: Ahh, you need to know, sometimes it is Byte Addressed, sometimes it is Word Addressed depending on the problem. In the above example, it is word addressed.

If it is byte-addressed, you need to decompose your offset furthermore into two parts: |Offset | = | Word Offset | Byte Offset |

Ahh, and the number of bits for the byte offset is always 2 or 3!!

• 32-bit word = 4 bytes per word = 2^2 → 2 bits for byte indexing
• 64-bit word = 8 bytes per word = 2^3 → 3 bits for byte indexing

Example

Physical address size is 28 bits, cache size is 32KB (or 32768B) where there are 8 words per block in a direct mapped cache (a word is 4B). The following choices list the tag, block index, block offset, byte offset fields from which you may select.

Related

• Set Associative Cache
• Fully Associative Cache