Fourier Series, Fourier Transform

Discrete Fourier Transform (DFT)

The discrete Fourier transform converts a finite sequence of equally-spaced samples of a function into a same-length sequence of equally-spaced samples of the discrete-time Fourier transform (DTFT), which is a complex-valued function of frequency.

The derivation from how you get to the DFT comes from Fourier Series.

We get that

$f_n={\sum }_{k=0}^{N-1}{F}_k{e}^{i\left(\frac{2\pi nk}{N}\right)}={\sum }_{k=0}^{N-1}{F}_k{W}^{nk}$

• Discrete data $f_n$ is expressed as a sum of coefficients $F_k$
• $W^{nk}$ is a Root of Unity where $W=e^{\frac{2\pi i}{N}}$

To find $F_k$, we’ll need another useful property of our Nth roots of unity: $W^{jk}{W}^{-jl}={\sum }_{j=0}^{N-1}{W}^{j(k-l)}=N{\delta }_{k,l}$

• where ${\delta }_{k,l}$ is the Kronecker Delta

We can now convert any data set into its Fourier coefficients, and back!

Inverse DFT: $f_n={\sum }_{k=0}^{N-1}{F}_k{W}^{nk}$

DFT: $F_k=\frac{1}{N}{\sum }_{n=0}^{N-1}{f}_n{W}^{-nk}$

The discrete Fourier transform is invertible.

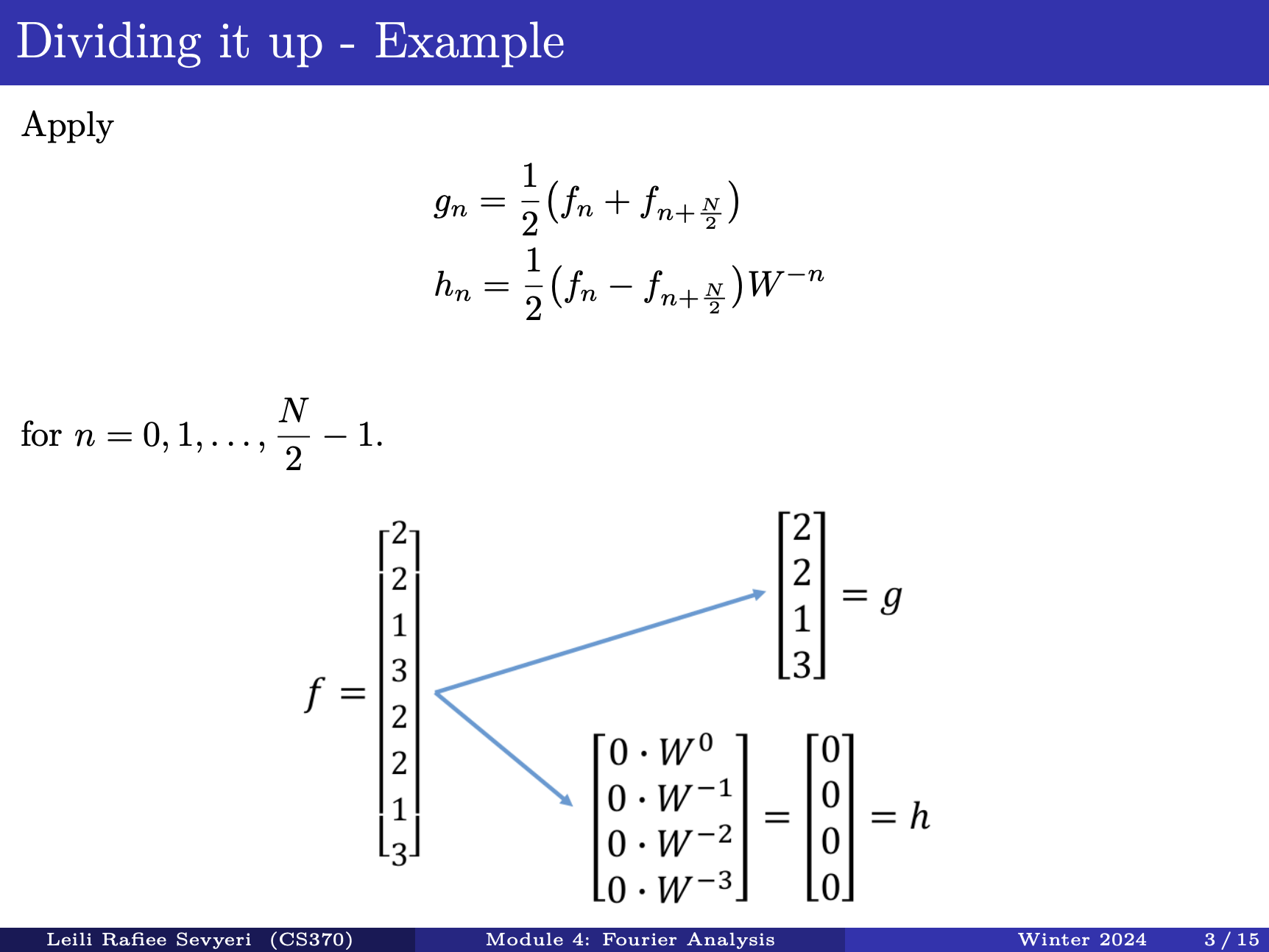
Splitting DFT into 2 to get to the FFT

The usual DFT of the sequence $f_n$ is

$F_k=\frac{1}{N}{\sum }_{n=0}^{N-1}{f}_n{W}^{-nk}$

• where $W$ is a complex exponential, see Root of Unity

We can express $f_n$ with DFTs of two new arrays of half the length $g_n=\frac{1}{2}(f_n+f_{n+\frac{N}{2}})$ $h_n=\frac{1}{2}(f_n-f_{n+\frac{N}{2}})W^{-n}$ where $n\in [0,\frac{N}{2}-1]$

Then, $F_{even}=G=DFT(g)$ and $F_{odd}=H=DFT(h)$

This is how we can use the FFT.

Lack of standardization

Properties

As consequences of the properties of $N$th roots of unity…

1. The sequence $\{F_k\}$ is doubly infinite and periodic. i.e., If we allow $k<0$ or $k>N-1$, the $F_k$ coefficients repeat.
2. Conjugate symmetry: If data $f_n$ is real, $F_k=\overline{F_{N-k}}$

Hence the $|F_k|$ are symmetric about $k=\frac{N}{2}$

Related

• Fast Fourier Transform