Fourier Series

Root of Unity

A root of unity is any complex number that yields 1 when raised to some positive integer power $n$.

Introduced in CS370 for the Fourier Transform.

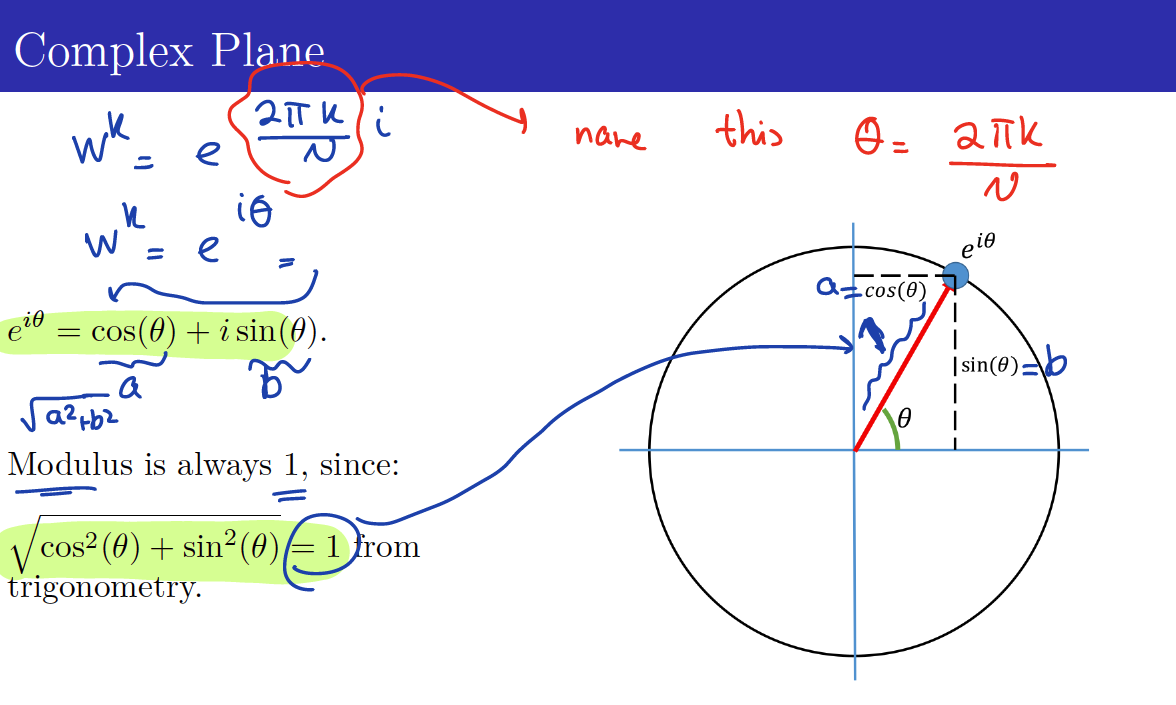
For notational convenience, we define: $W=e^{\frac{2\pi i}{N}}$

W is a N-th root of unity

$W$ is an $N$-th Root of Unity, since it satisfies $W^N=e^{2\pi i}=1$

Since $W=e^{\frac{2\pi i}{N}}$ then $W^k=e^{\frac{2\pi ik}{N}}$

But how do you actually compute this? Remember your trig circle

$W^k=e^{\frac{2\pi ik}{N}}=\cos \left(\frac{2\pi k}{N}\right)+i\sin \left(\frac{2\pi k}{N}\right)$