Double Integrals

We cannot change the order of integration so easily.

Integration of Scalar Fields

Think of this in 3D, where $f(x,y)$ is coming towards you in the $z$-axis. So the integral gives the volume.

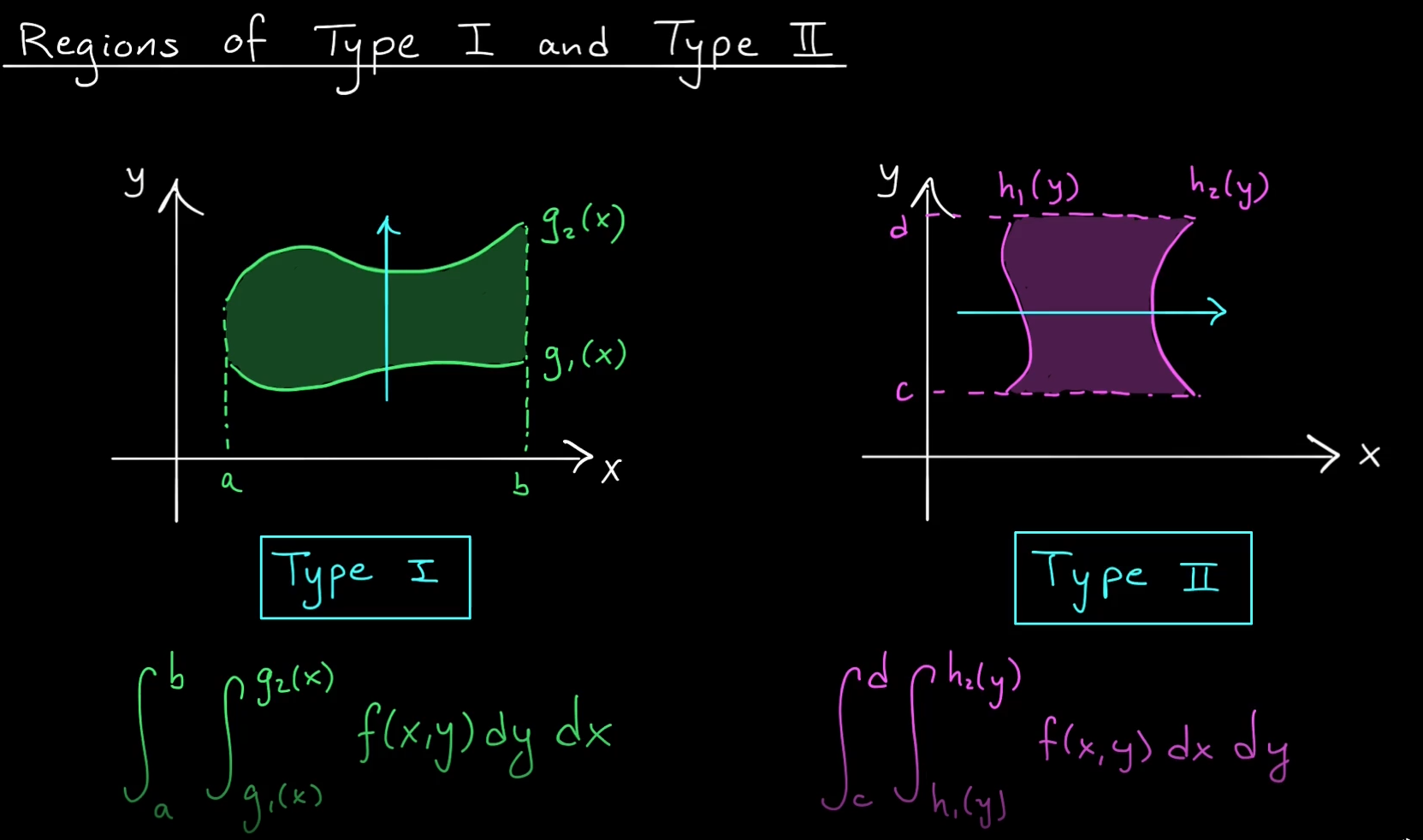
Region of Type I

${\int }_{R}f(x,y)dA={\int }_a^b{\int }_{g(x)}^{h(x)}f(x,y)dydx$

Region of Type II

${\int }_{R}f(x,y)dA={\int }_c^d{\int }_{g(y)}^{h(y)}f(x,y)dxdy$

Double Integrals in Polar Coordinates

We rewrite the integrand by setting $x=\rho \cos \varphi \text{and}y=\rho \sin \varphi$ so $f(x,y)=(\rho \cos \varphi ,\rho \sin \varphi )$

${\iint }_{R_{xy}}f(x,y)dxdy={\iint }_{R_{\rho \varphi }}f(\rho \cos \varphi ,\rho \sin \varphi )\rho d\rho d\varphi$

Triple Integrals

See Coordinate System.

In general, we double and triple integrals to calculate areas and volumes. The general notation is given by

$\text{Area}={\iint }_{R}dA$ $\text{Volume}={\iiint }_{D}dV$