Coordinate System §

This was focused on heavily for ECE106, and also learned in MATH119.

See [[notes/Differentials#Differential Length Element|Differentials#Differential Length Element]]

See Coordinate Frame if you’re referring for robotics.

Cartesian Coordinate §

Cartesian coordinates are defined by 3 vectors with directions given by 𝑥̂, 𝑦̂, 𝑧̂.

In math, we use 𝑖̂, 𝑗̂, 𝑘̂. 𝐴⃗ in terms of the coordinate system will be given as: $A⃗=Ax\hat{x}+Ay\hat{y}+Az\hat{z}$

where $A_x$ is the distance you move in 𝑥̂ direction, $A_y$ is the distance you move in 𝑦̂ direction and $A_z$ is the distance you move in 𝑧̂ direction. [[notes/Differentials#Differential Surface Elements|Differentials#Differential Surface Elements]]

Polar Coordinates §

We have two vectors which define the polar coordinates, vector 𝑟̂ which changes the radius of the compass and vector $\hat{\varphi }$ which changes the angle $\varphi$. $\hat{\varphi }$ is perpendicular to $\hat{r}$ (and is thus, orthogonal) and by conventions changes the angle $\varphi$ counter-clockwise. $\hat{\varphi }$ is called the azimuthal vector.

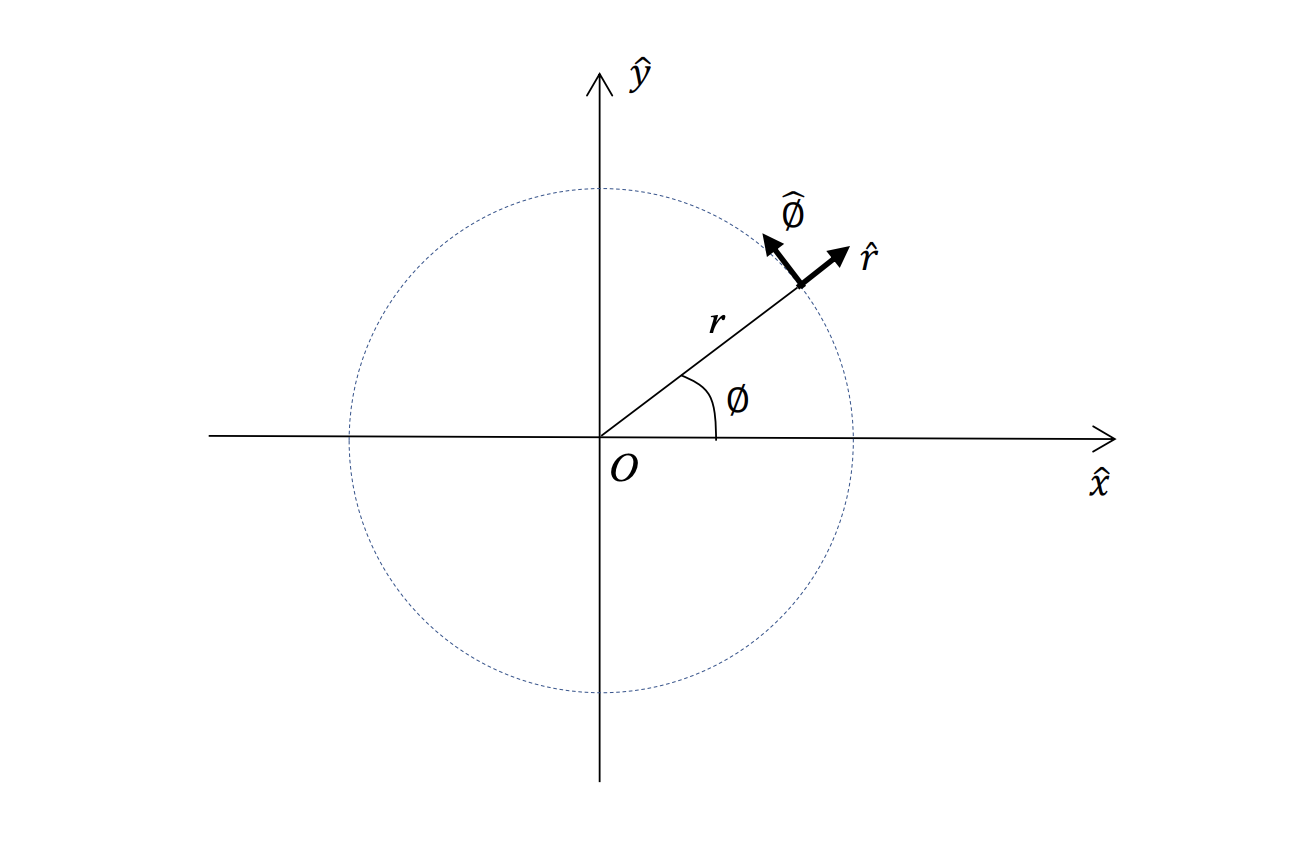
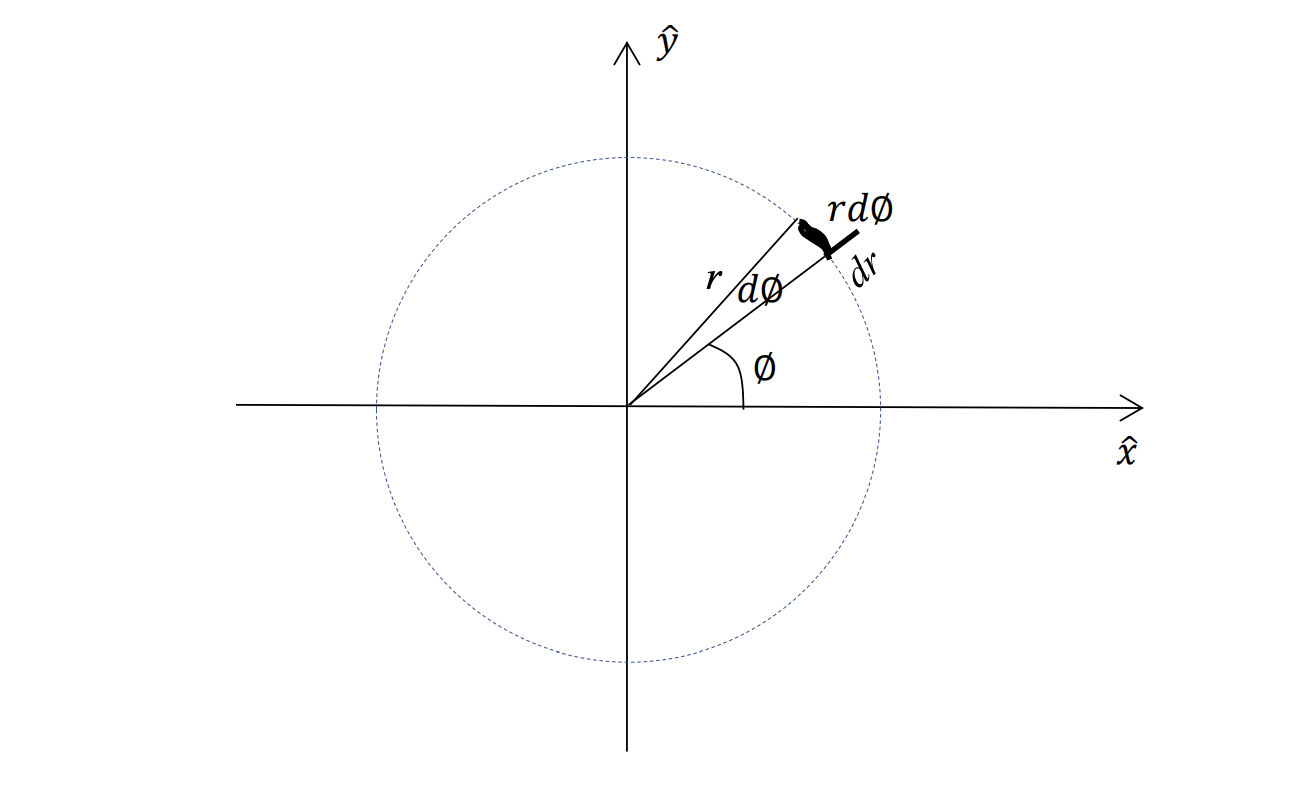
Intuition for Polar Coordinate

I get confused easily because there is an extra $r$ in $rdrd\varphi$ for the differential area element, compared to cartesian coordinates which only has $dxdy$.

This is because the area, one of them is $dr$, and the arc is given by $rd\varphi$, NOT $d\varphi$, $\varphi$ is just an angle.

Cylindrical Coordinate §

Cylindrical coordinates are basically polar coordinates in 3D.

We follow the left-hand rule and thus, 𝑟̂ is the first vector, ∅̂ is the second vector and 𝑧̂ is the third vector.

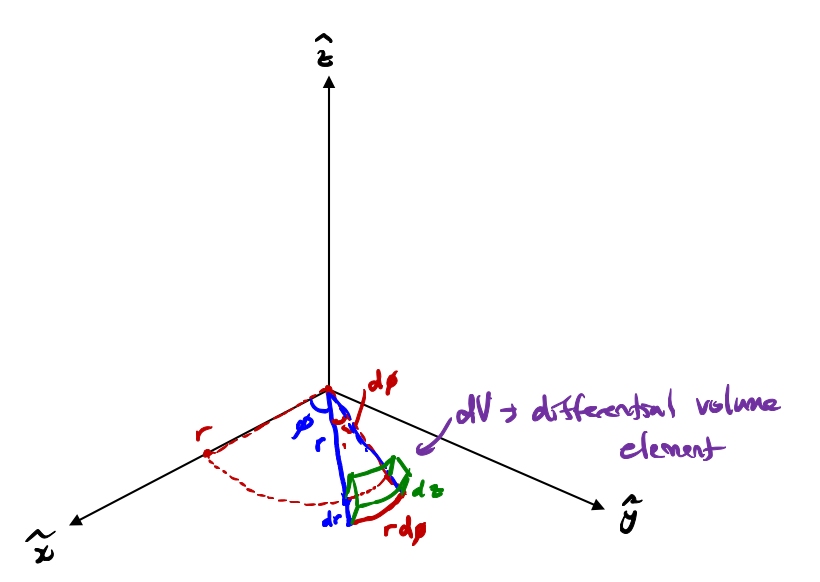
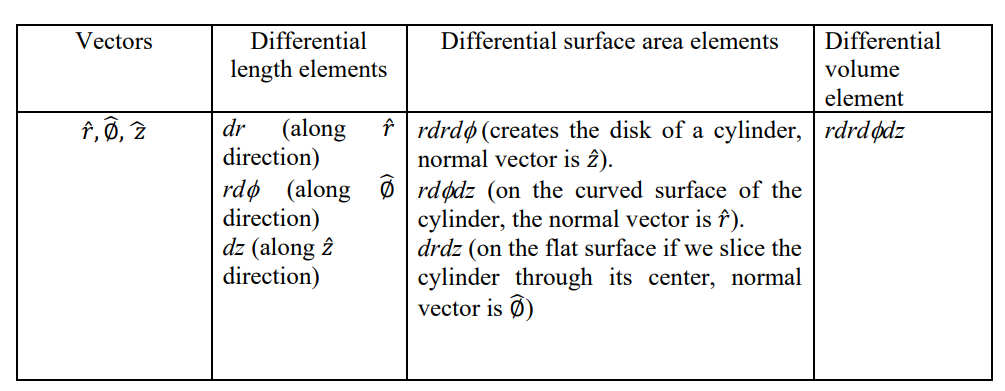
Conversion from Cartesian to Polar Coordinates §

We simply let $x=r\cos \varphi \text{and}y=r\sin \varphi$

Spherical Coordinate §

We will make the z-axis as a principle axis of symmetry. So the sphere will be symmetrically created around the z-axis. We introduce a new vector, 𝜃̂ which changes the angle of the line with respect to the z-axis. This vector is called the polar vector.

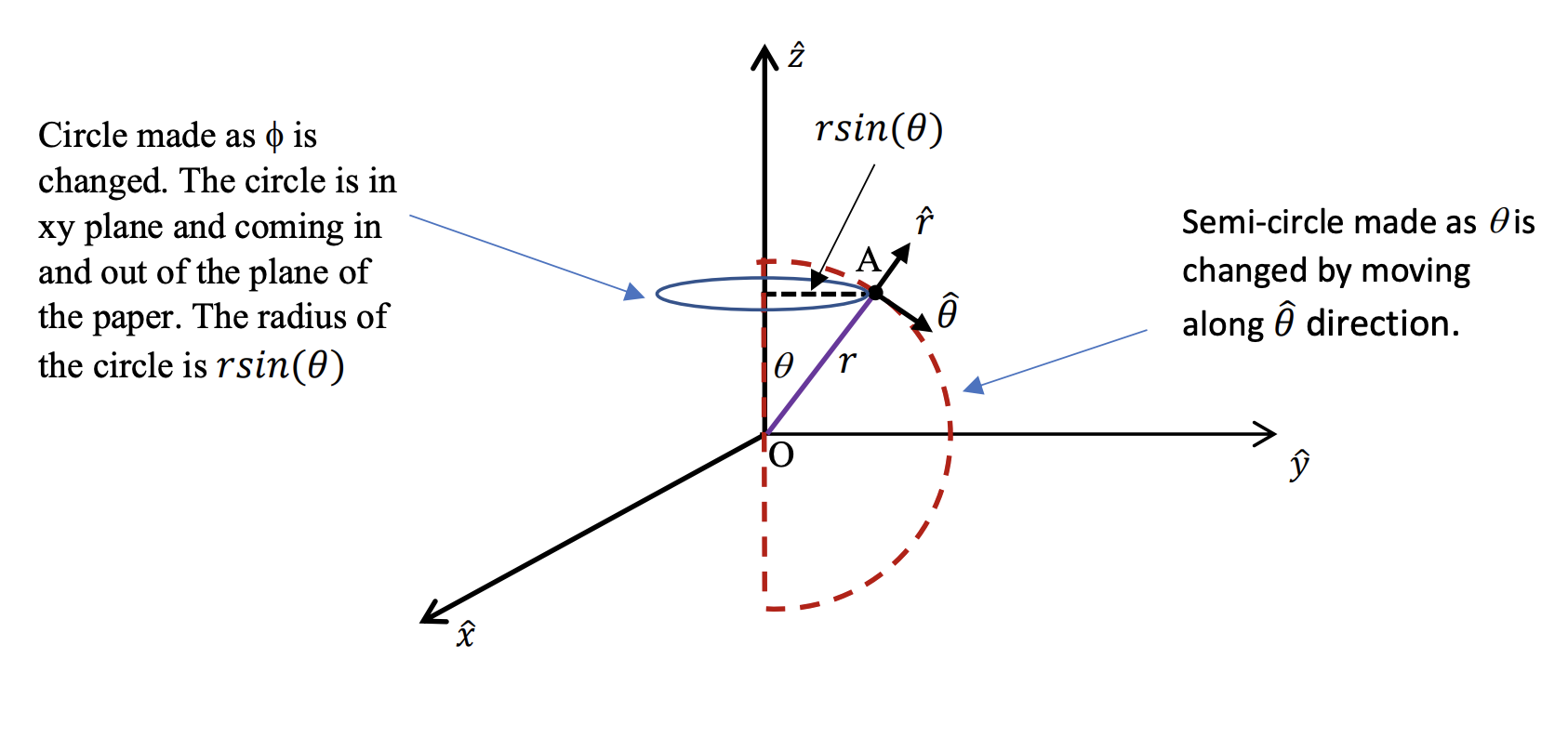
Understand the 3 differential elements, should be easy now

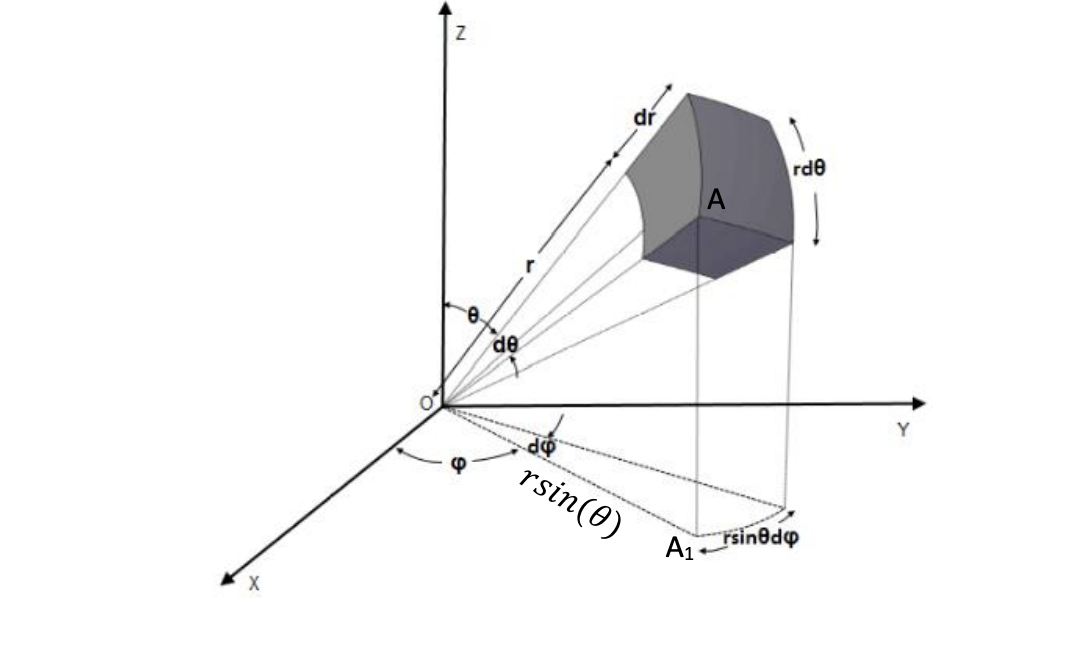
Danger

In spherical coordinates, r is the distance of the point from the origin. In cylindrical coordinates, it is the perpendicular distance of the point from the z-axis.

Related §

• Moment of Inertia