Electric Potential

Electric potential always has a reference point.

When we talk about electric potential difference, we usually compare the difference between points A and B.

Video: Electric Potential: Visualizing Voltage with 3D animations.

Intuition

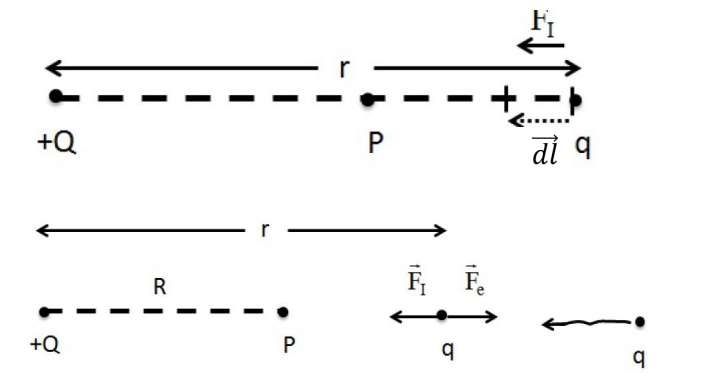
To understand electric potential at point $P$, we do the following thought experiment. We bring a charge $q$ from $\infty$ and bring it to point $P$. It experiences electric force as we bring it closer. The work is given by $W_I={\int }_{\infty }^{P}d{W}_I={\int }_{\infty }^P-{\vec{F}}_E\cdot d\vec{l}={\int }_{\infty }^P-q\vec{E}\cdot d\vec{l}$

title: Reference
We have defined potential with the work I do to move the charge; not the work that the electric field $\vec{E}$ does. $W_I = -W_E$

We thus assume that $V_{\infty }=0$ since this is our reference.

Electric potential at point $P$ ($V_P$) is then defined as work done per unit positive test charge as the test charge approaches 0. $V_P={\lim }_{q\to 0}\frac{W_I}{q}=-{\int }_{\infty }^P\vec{E}\cdot d\vec{l}$

We also realize that path does not matter, as electrostatic force is a conservative force. So $\vec{E}\cdot d\vec{l}=Edr$. Revisit Electric Field Calculations $V_p=-{\int }_{\infty }^{P}Edr=\frac{kQ}{r}$

To find the electric potential at point $P$ with distance $r$ affected by $Q$, we use $V_p=-{\int }_{\infty }^r\frac{kQ}{r^2}dr=\frac{kQ}{r}$

Misc

Electric Potential Energy is the interaction energy of a charged particle with the source charges.

$V=\frac{kQ}{r}$ $V=\int \frac{kdQ}{r}$

For parallel plate calculations, a single parallel plate Electric field is given by $E=\frac{\lambda }{2ϵ}$ Two parallel plates is, $E=\frac{\lambda }{ϵ}$ $\Delta V=Ed$

title: Relationship between Electric Potential and Electric Field
The most intuitive way to understand electric potential is to understand its relationships to electric fields.
 
Electric potential is a property of source charges. It is a scalar field and related to the electric field (a vector field) by:
$$\vec{E} = - \nabla V$$

- The Electric Force is a [[Conservative Force]]. Electric Potential is independent of the path taken.

Electric Potential Difference (Voltage)

Voltage is simply electric potential difference. Voltage = electric potential difference $\Delta V=\frac{\Delta U}{q}$

Knowing the electric potential in a region of space allows us to determine whether a charged particle speeds up or slows down as it moves through that region.

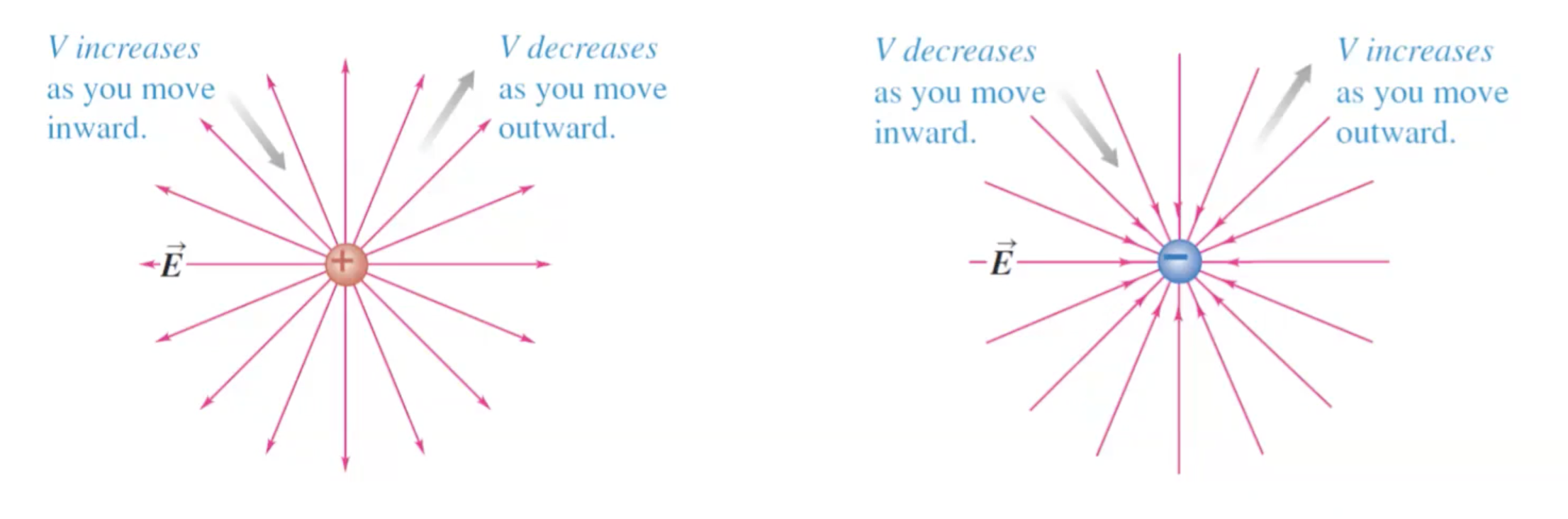
A positive charge slows down as it moves into a region of higher electric potential. Here is a nice table to understand the behaviors on charges in varying electric potentials.

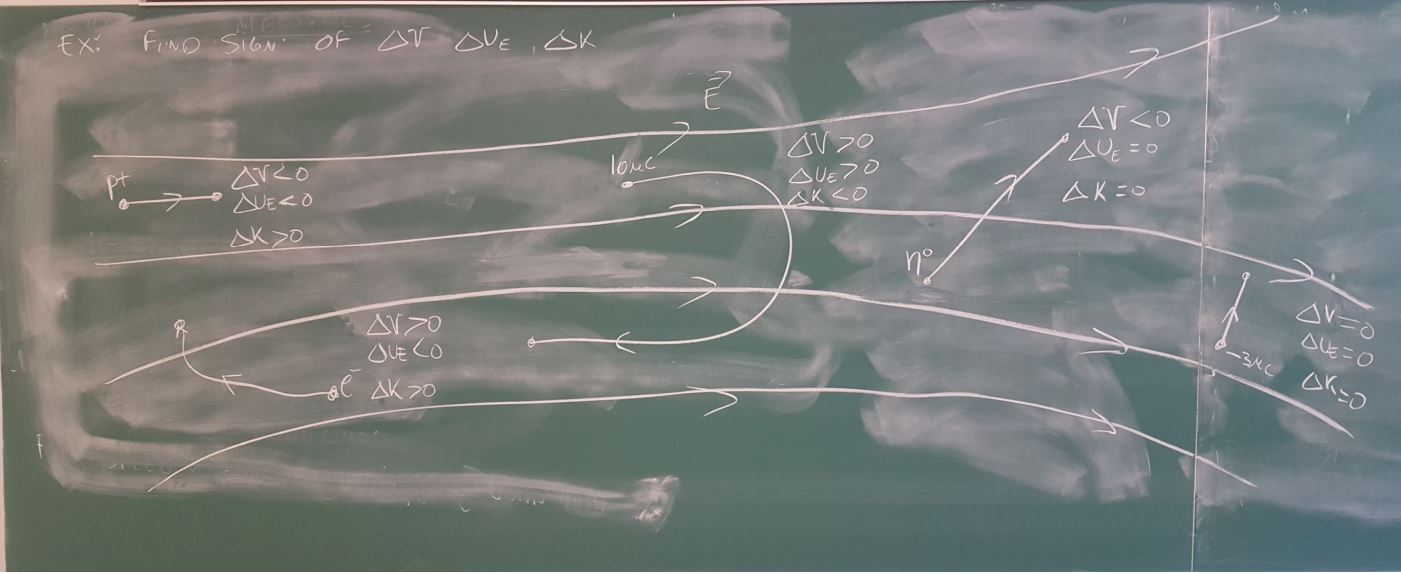
Electric Potential and Electric Potential Energy

Electric Potential is Electric Potential Energy per unit charge: $V=\frac{U}{q}$

• measured in volts

Electric Potential inside a Capacitor

Electric Potential of Many Charges

What happens to the electric potential when there are many source charges? Well, it’s simple, we just add each of them up. Electric potential, like electric field, obeys the principle of superposition.

${\sum }_{i<j}^5\frac{K{q}_i{q}_j}{r_{ij}}$

Electric Potential when you connect two spheres

Essentially, the two spheres stabilize once the two spheres reach the same potential. $V_1=V_2$ $K{q}_1/r_1=k{q}_2/r_2$