Gradient Descent

Gradient descent is an optimization algorithm which is commonly-used to train machine learning models and neural networks.

You should be familiar with Partial Derivatives first.

Let $J(w)$ be a differentiable function of parameter/weights vector $w$. Define the gradient of $J(w)$ to be ${\nabla }_{w}J(w)=(\frac{\partial J(w)}{\partial w_1}⋮\frac{\partial J(w)}{\partial w_n})$

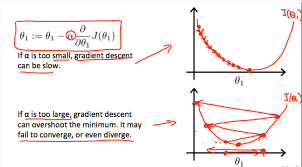
To find a local minimum of $J(w)$, adjust $w$ in direction of negative gradient: $∆w=-\frac{1}{2}\alpha {\nabla }_{w}J(w)$ where $\alpha$ is the learning rate (step-size parameter).

The step size is also called the learning rate.

while True:
  weights_grad = evaluate_gradient(loss_fun, data, weights)
  weights += - step_size * weights_grad # perform parameter update

There are two ways to compute the gradient:

• Numerical Gradient: Not practically feasible. See page for code.
• Analytical Gradient: Uses calculus.

Now, Backpropagation comes into the picture when we look at how to compute the evaluate_gradient function. For SVM for example, we have a fixed analytical gradient that we calculated, but we want to be able to do this for any function.

Challenges

1. Running into a local minima / saddle point → fix those challenges by adding stochasticity.

Related

• Mini-Batch Gradient Descent
• Stochastic Gradient Descent

WAIT, Serendipity, we saw this sort of idea in E&M with Electric Potential Energy, remember the lab. We saw that the gradient represents the change in potential (wait how do Electric Field, Electric Potential, and Electric Potential Energy relate?)

Optimizer

SGD:

momentum update

# Vanilla Gradient Descent
x += - learning_rate * dx
 
# Momentum update
"""
- We build up velocity along shallow directions.
- Velocity becomes damped in steep direction due to quickly changing sign.(you can initialize v=0)
"""
v = mu * v - learning_rate * dx # mu * v is like the friction, mu is a hyperparameter, mu = 0.5 or 0.9
x += v
 
# Nesterov Momentum update (this is a trick to get a look-ahead)
v_prev= v
v = mu * v - learning_rate * dx
x += -mu * v_prev + (1 + mu) * v
 
# Adagrad
cache += dx ** 2
x += - learning_rate * dx / (np.sqrt(cache) + 1e-7)
 
# RMSProp (improvement of Adagrad)
cache += decay_rate * cache + (1-decay_rate) * dx ** 2
x += - learning_rate * dx / (np.sqrt(cache) + 1e-7)
 
# Adam (combines momentum and RMSProp)
m = beta1*m + (1-beta1)*dx # update first moment
v = beta2*v + (1-beta2)*(dx**2) # update second moment
m /= 1 - beta1**t # correct bias (only relevant in the first few iterations)
v /= 1 - beta2**t # ""
x += - learning_rate * m / (np.sqrt(v) + 1e-7)

As you scale up your network, it looks more like a bowl. Local minimum become less and less of an issue. It only really happens with small networks. - Andrej Karpathy

Adam is the default choice. See original paper: https://arxiv.org/abs/1412.6980v8

Use exponential decay for learning rate. $\alpha ={\alpha }_0{e}^{kt}$

Gradient Descent from first principles

I thought I understood gradient descent, but it’s very easy to forget the underlying motivations. Like sure, you can just say that you make a gradient update in the direction.

My understanding is mainly written in Backpropagation. But rewriting some ideas as a refresher here.

Let’s say we want to estimate parameters for a linear model $\hat{y}=ax+b$:

• That is, we want to get parameters $a,b$ that fit best to an input set of $(x_i,y_i)$ values
• Of course, you can do this easily with Linear Regression, but let’s be fancy and use gradient descent to do parameter updates

We define our loss function as the squared error: $L=(y-\hat{y}{)}^2$

• $\hat{y}$ is our estimated value, $y$ are measurements

What happens with y?

Remember that we are taking partial derivatives. $y$ and $\hat{y}$ are both variables that represent some variables.

• However, we keep the parameters fixed and play around with various y values

We want to update parameters $a,b$ is updated based on the gradient to minimize our loss. The update would be simply $a\leftarrow a+\alpha \cdot \frac{\delta L}{\delta a}$ $b\leftarrow b+\alpha \cdot \frac{\delta L}{\delta b}$

• $\alpha$ is just some learning rate

So we have the following two functions:

• $L=(y-\hat{y}{)}^2$
• $\hat{y}=ax+b$

We apply the chain rule to apply a partial derivative gradient $\frac{\delta L}{\delta a}=\frac{\delta L}{\delta \hat{y}}\frac{\delta \hat{y}}{\delta a}=(2(y-\hat{y})\cdot (-1))\cdot (x)=-2(y-(ax+b))\cdot x$ $\frac{\delta L}{\delta b}=\frac{\delta L}{\delta \hat{y}}\frac{\delta \hat{y}}{\delta b}=(2(y-\hat{y})\cdot (-1))\cdot (1)=-2(y-(ax+b))$

• If you’re not sure about how I got this, revisit your partial derivatives

Usually, updates are done in small batches of data, but for the sake of simplicity, assume we are only reading in a single value before doing an update.

Wait, do we care about \frac{\delta L}{\delta a} or \frac{\delta a}{\delta L}?

$\frac{\delta a}{\delta L}$ doesn’t really make sense does it? We want to find a parameter $a$ such that there is a minima at $L$.

It’s like having a function $y=x^2$. What is $\frac{dx}{dy}$? Well its just the inverse, but is that useful to us?

• We care about $\frac{dy}{dx}$ because that tells us how $y$ changes as we change $x$, not how $x$ changes as we change $y$ (because $y$ is the output, we can’t really modify it)

If you did a gradient update of $a$ with $\frac{\delta a}{\delta L}$, what would happen?

• Incorrect results, that tells how $a$ changes as you change $L$, however we want to see how $L$ changes as you change $a$

I was having trouble visualizing gradient descent updates. Like if you plot your function, and observations are just points, you’re actually looking at a different gradient points.

• remember that the set of parameters represent the entire function, not a particular point
• So the idea is that with gradient descent, if you sample a wide enough variety of points, as you update your gradients, you are going to get closer and closer to points that represent the function

I’m having trouble visualizing this. Ahh actually I can see it