Homogeneous Linear Equation
A homogeneous linear equation is a linear equation where the constant term is zero.
A system of homogeneous linear equations is a collection of finitely many homogeneous equations.
Example: Solve the homogeneous linear system
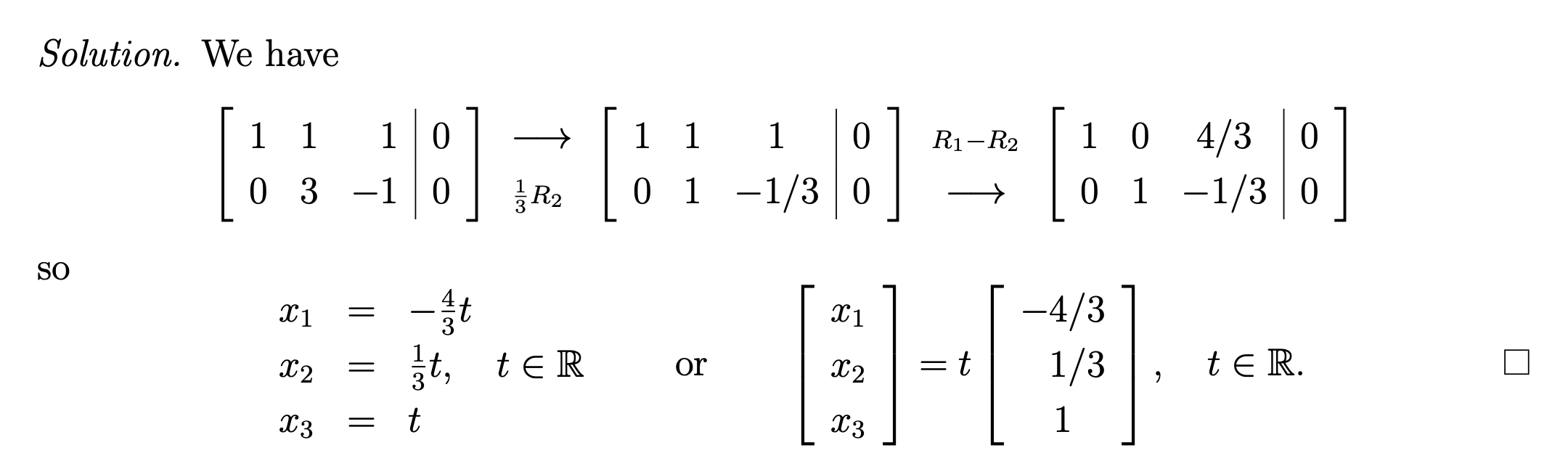
Relationship with Non-Homogeneous System
The solution to the associated homogeneous system tells us a lot about the solution of the original non-homogeneous system .
Continuing on the example above, try to solve the non-homogeneous linear system (where we changed the constants to be non-zero):
x_1 + x_2 + x_3 = 1\\ [3pt] 3x_2 - x_3 = 2\\ [3pt] \end{aligned}$$ ![[attachments/Screenshot 2023-01-21 at 5.07.47 PM.png]] Thus, you realize the following: ![[attachments/Screenshot 2023-01-21 at 5.05.01 PM.png]] ### Related - [[notes/Homogeneous Coordinate|Homogeneous Coordinate]]