Linear Equation

A linear equation in $n$ variables is an equation of the form $a_1{x}_1+a_2{x}_2+\cdots +a_n{x}_n=b$ where

• $x_1,...,x_n\in \mathbb{R}$ are the variables (unknowns)
• $a_1,\dots ,a_n\in \mathbb{R}$ are coefficients
• $b\in \mathbb{R}$ is the constant term

To solve systems of linear equations, we use Matrix.

Next, see Homogeneous Linear Equation.

System of Linear Equations

If we have a set of $m$ linear equations, we can write it down in matrix form, i.e.: $Ax=b$

• where $A_{m\times n}$ is a matrix

This is very fundamental

Systems of linear equations are used eveywhere.

The solution is given by $x=A^{-1}b$

• See Determinant for how to compute $A^{-1}$

How many solutions are there? Is there no solution, 1 solution, or an infinite amount of solutions?

• It seems like there is only 1 solution, because the matrix inverse is unique. So $A$ is only invertible when there is a single solution. When there are multiple or no solutions, $A$ cannot be invertible. Because if there was, then there would be multiple matrix inverses. Which is a contradiction. If there are no solutions but a matrix inverse exists, that is also a contradiction

We can first examine A. Remember the RREF stuff.

So there are 2 ways you can visualize $Ax=b$.

1. You can see it row-wise, where you have a dot product between the $i$-th row of $A$ and $x$, where $b_i={\sum }_j{A}_{i,j}{x}_j$.

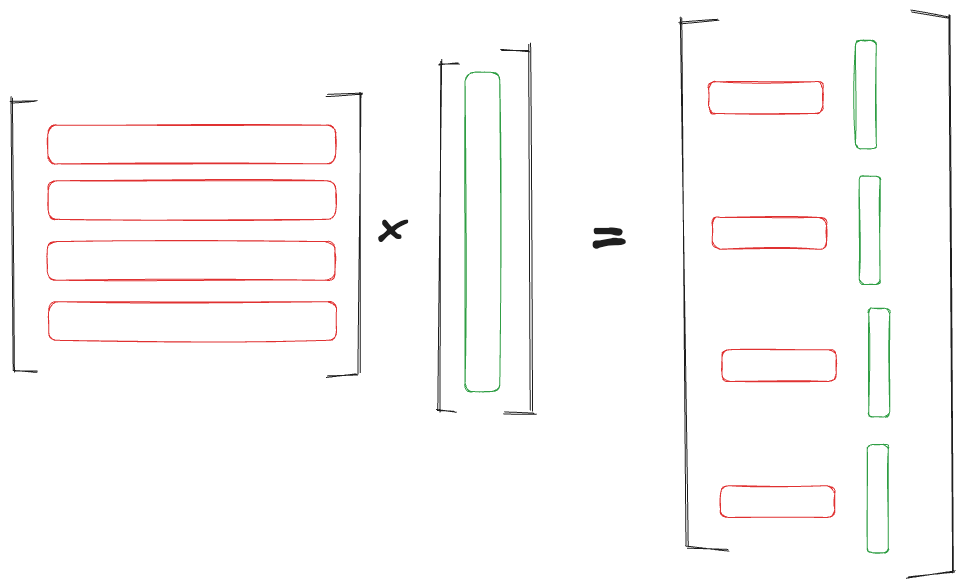
2. You can see it as a column-wise linear combination, where you have $b=x_0{A}_{0,:}+x_1{A}_{1,:}+\dots$

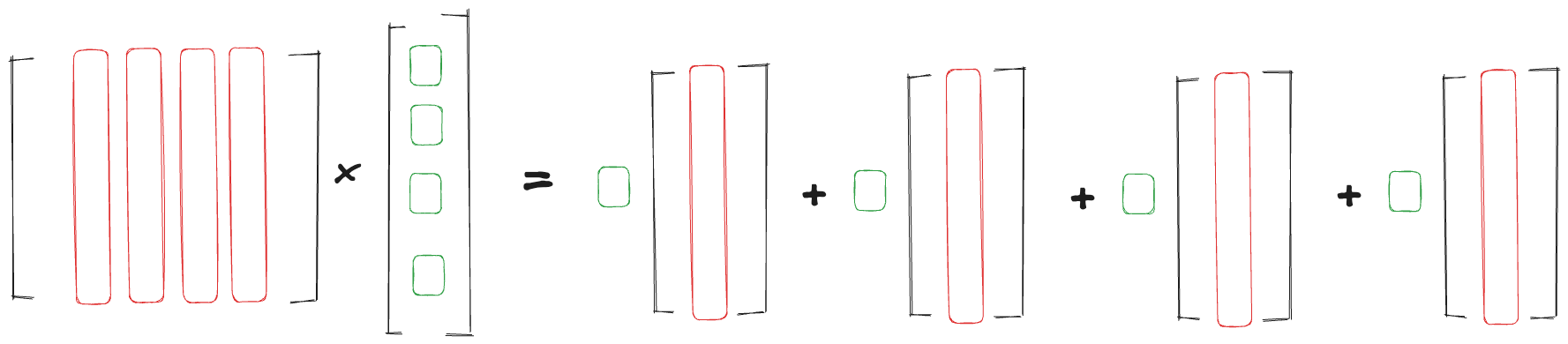
• note that this only works because the second is a column vector

With this way of seeing the matrix multiplication, you can see that a solution only exists when $b$ is the in Column Space of $A$!!

Abstract

Determining whether $Ax=b$ has a solution thus amounts to testing whether $b$ is in the span of the columns of $A$.

Interview question

For $Ax=b$ to have a solution $x$, what are the requirements of $A$?

• If you want it to work for all $b\in {\mathbb{R}}^m$, then the column space of $A$ must be ${\mathbb{R}}^m$
• $A$ must have a least $m$ vectors for that to work.
• If $A$ has more than $m$ vectors, then $A$ is not linearly independent
• So $A$ must be exactly $m\times m$ for it to have an inverse

• Also Gaussian Elimination!!