Min-Hashing

Min-Hashing applies Locality-Sensitive Hashing for Jaccard Distances.

Problem Setup - Near Neighbours

Problem:

• $S$ – Set of Objects
• $D(a,b)$ – Distance from object $a$ to $b$
• $t$ – maximum distance threshold Goal: Find all unordered pairs $(a,b)$ s.t. $D(a,b)\le t$.

• The The naïve approach: compute all pairs in $O(n^2)$

But with min-hashing, we can achieve $O(n)$ performance!

Some examples of real-world problems for near neighbours

• Template Based Protein Folding
• Document similarity

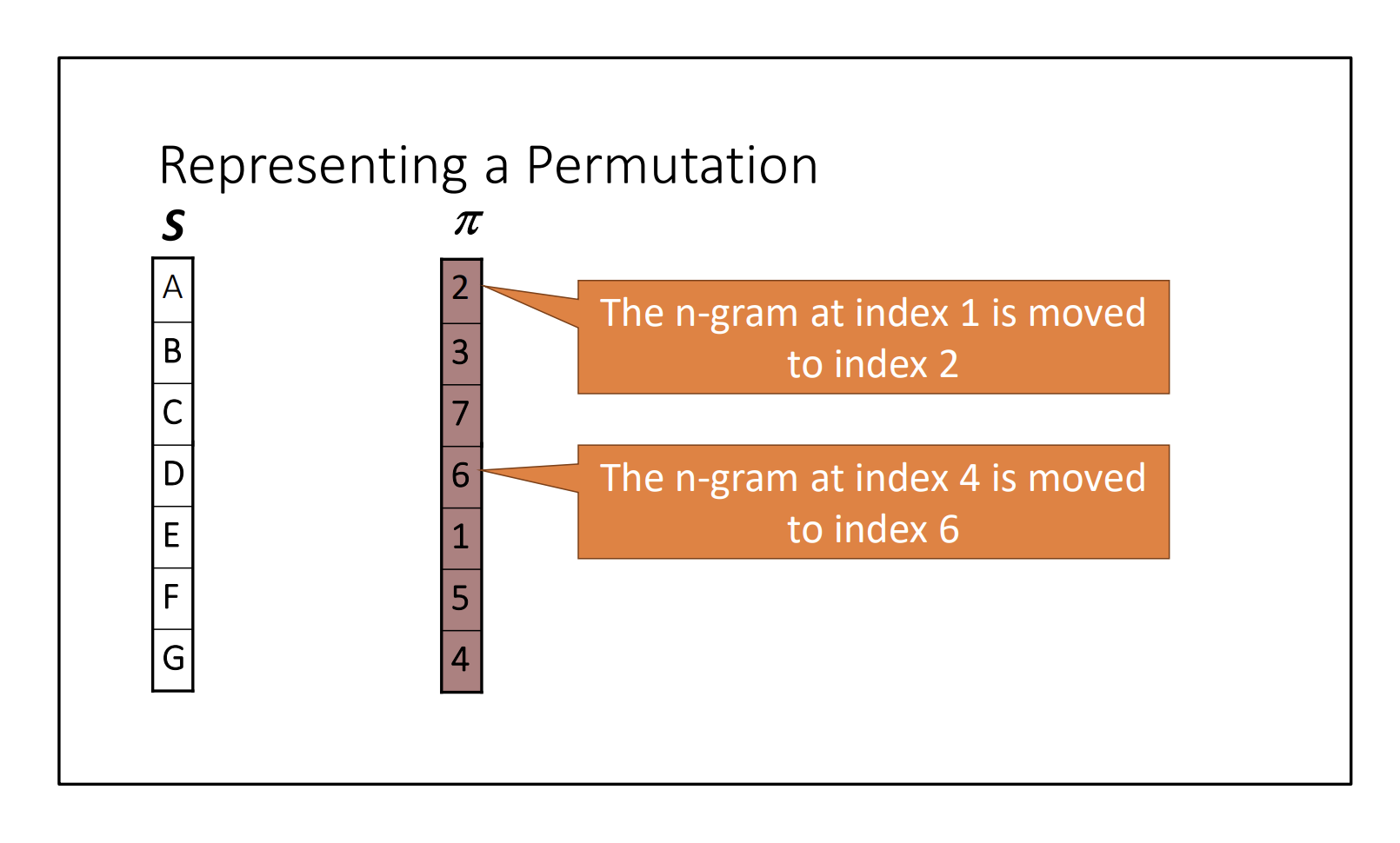
Min-hashing (two views) Imagine you have a random permutation $\pi$.

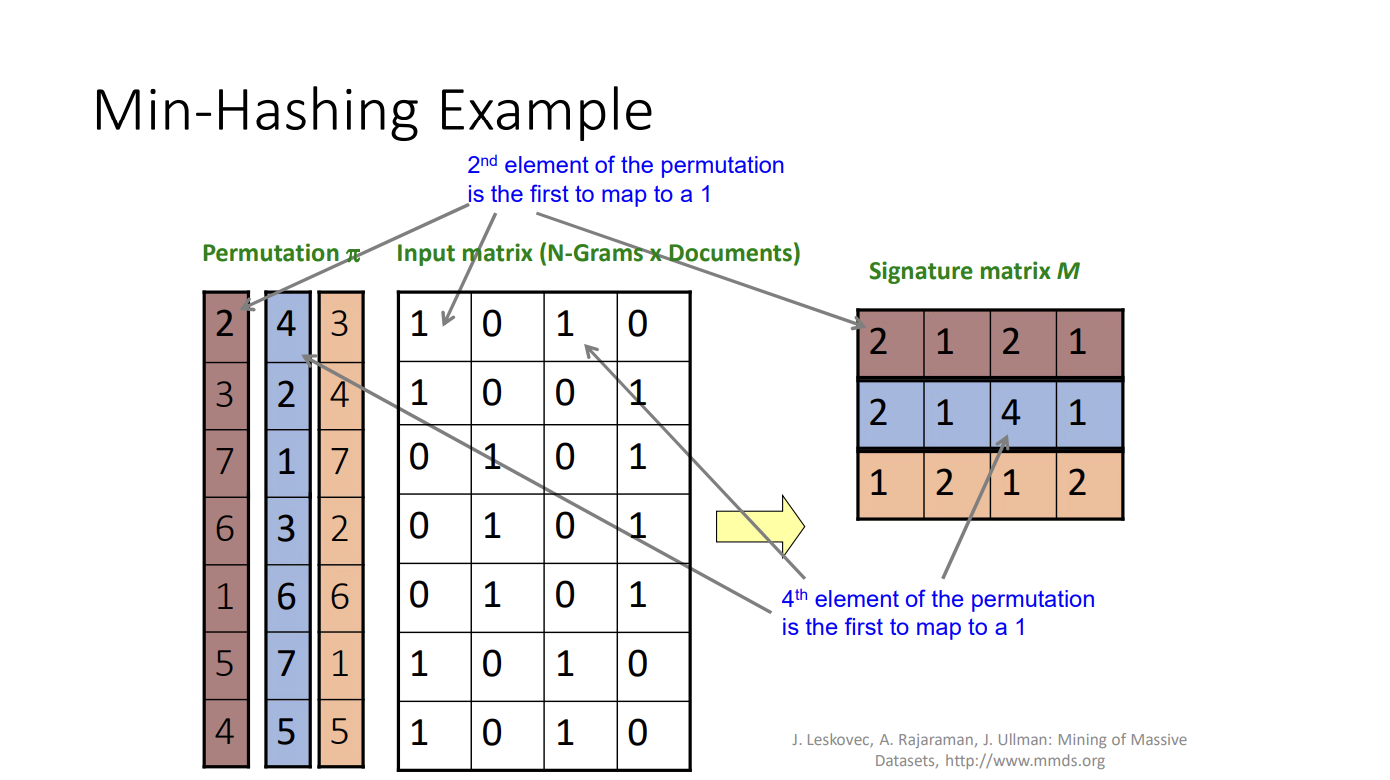
• Do this exercise, you will understand how the signature matrix is calculated, but it’s pretty straightforward

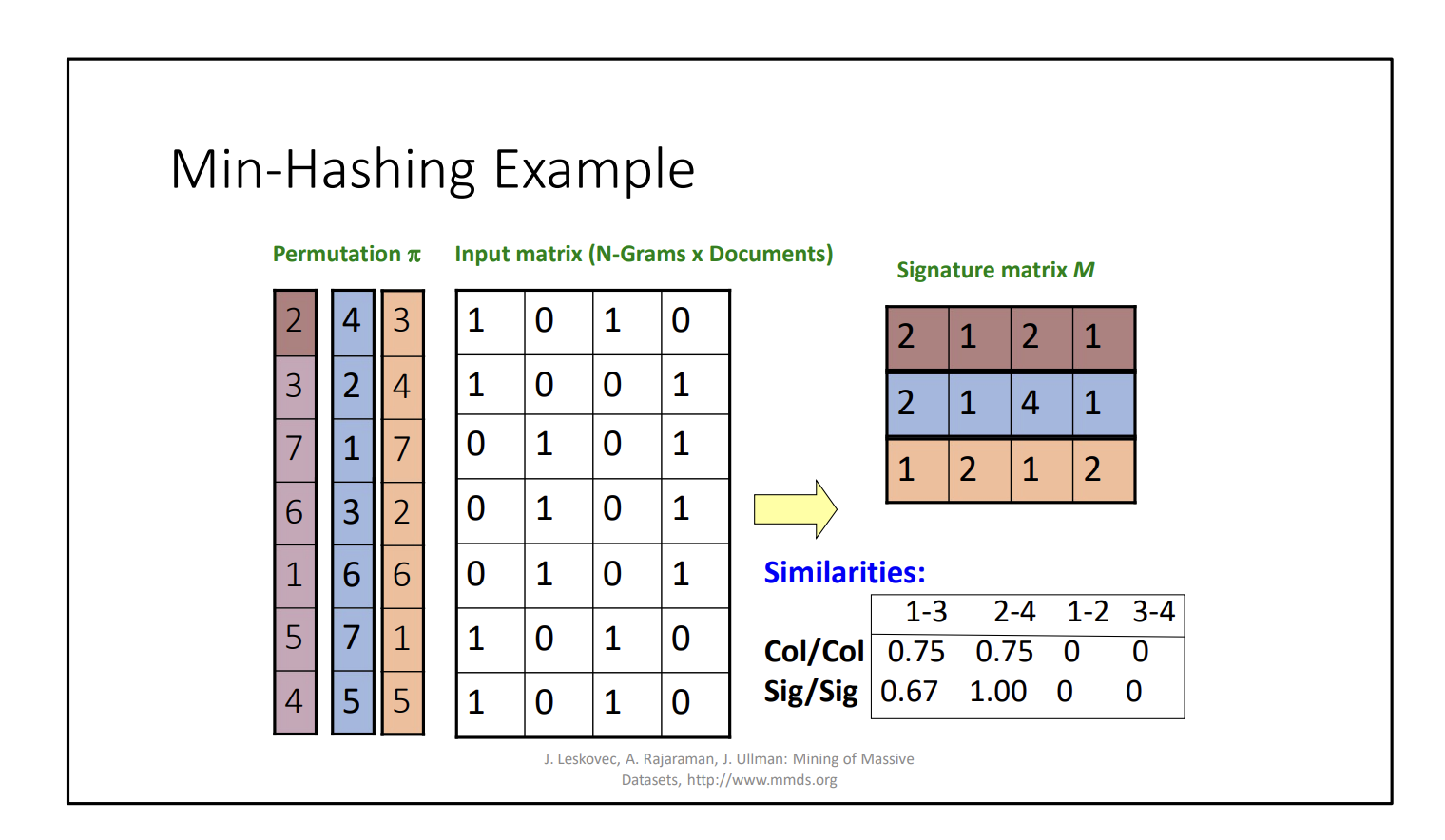
Abstract

• Step 1 – convert each document into n-grams
• Step 1.1 – convert each unique n-gram into an integer
• Step 2 – Generate a set of universal hash functions
• Step 3 – For each document, compute the short signature vector
• Step 4 – Pick values of R, B to tune to the false-positive and/or false negative rates you want
• Step 5 – Hash each of the B bands for each document to find candidate pairs
• Step 6 (technically optional, but absurd to skip) – Confirm the signatures are similar
• Step 7 (more optional) – Confirm the documents are similar