One-to-One and Onto Function

One-to-one function (also called injective): In a one-to-one function, given any $y$ there is only one $x$ that can be paired with the given $y$.

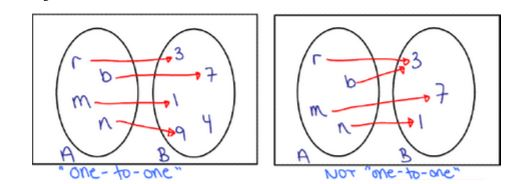
• If a function is injective, then it is an Invertible Function

Onto function (also called surjective): An onto function is such that for every element in the codomain there exists an element in domain which maps to it.

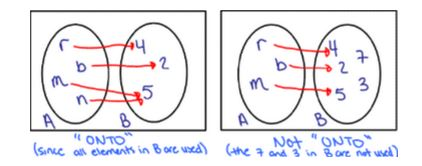
A bijective function is both one-to-one and onto.

Formal Definition from SE212

Defined from the perspective of a Binary Relation.

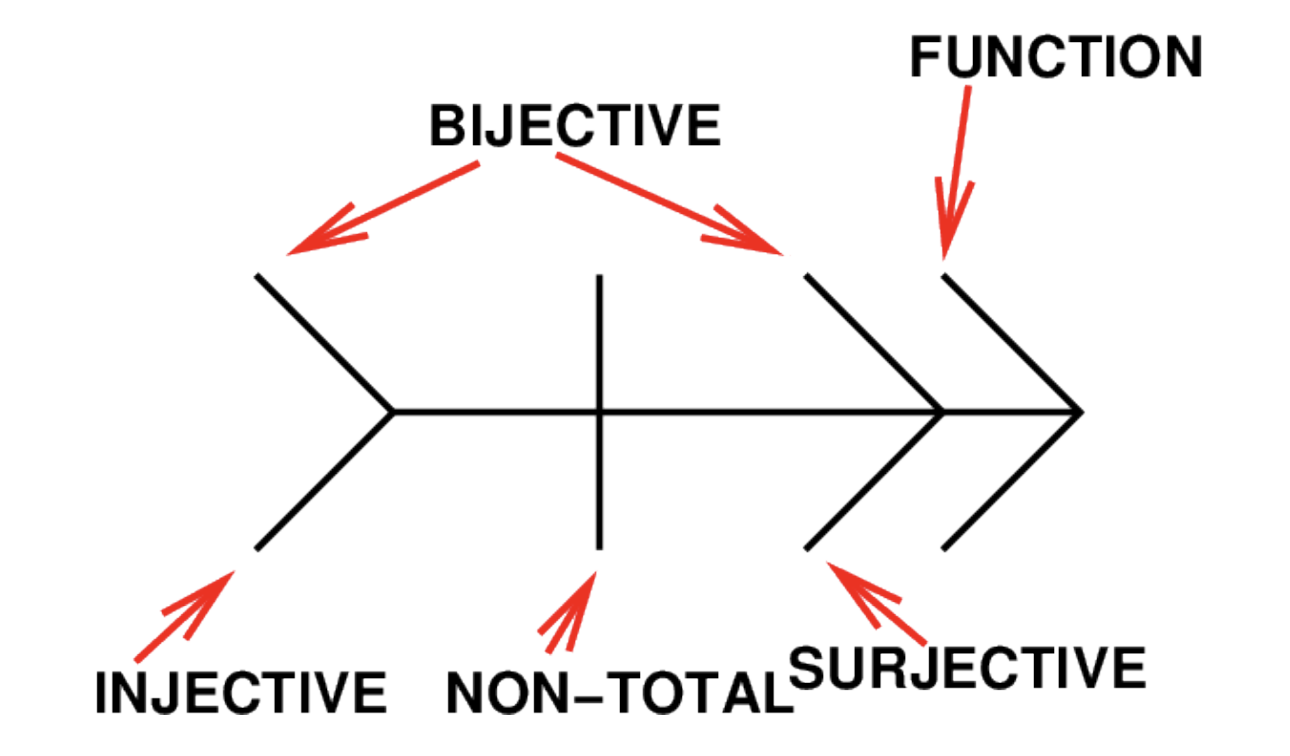
Surjective Function (Onto)

• A function f from set $A$ to set $B$ is surjective if every element of $B$ is matched with some element of the domain of $f$. A function $f$ from set $A$ to set $B$ is surjective if and only if: $\forall b:B•\exists a:A•f(a)=b$
• $f$ is surjective if every element of $B$ appears AT LEAST ONCE as the second component of an ordered pair in $f$
• For a function to be surjective, the domain must have at least as many elements as the range.

Injective (One-to-one) Functions

• A function is injective if its inverse is a function. This means that each element of the domain maps to a unique element of the range. A function $f$ from set $A$ to set $B$ is injective if and only if: $\forall x,y:A•f(x)=f(y)\Rightarrow x=y$ An injective function $f$ is one such that an element of B appears AT MOST ONCE as the second component of an ordered pair in $f$

Bijective Function

A bijective function is one that is both surjective (onto) and injective (one-to-one).

MATH239

Learning this a THIRD time.

Definition 1.10. Let $f:A\to B$ be a function from a set $A$ to a set $B$. • The function f is surjective if for every $b\in B$ there exists an $a\in A$ such that $f(a)=b$. • The function f is injective if for every $a,a^{\prime }\in A$, if $f(a)=f(a^{\prime })$, then $a=a^{\prime }$ • The notation $A\leftrightarrow B$ indicates that there is a bijection between the sets A and B